题目内容
 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和D(5,0).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和D(5,0).(1)求该二次函数的解析式;
(2)直接写出该抛物线的对称轴及顶点C的坐标;
(3)点B是该抛物线与y轴的交点,求四边形ABCD的面积.
考点:待定系数法求二次函数解析式,二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)利用待定系数法把点A(-1,0)和D(5,0).代入二次函数y=ax2-4x+c中,可以解得a,c的值,从而求得函数关系式;
(2)根据(1)中的函数解析式,利用配方法求出对称轴及顶点坐标.
(3)根据(1)中的函数解析式,求得B的坐标,然后根据S四边形ABCD=S△OAB+S△OBC+S△OCD即可求得四边形ABCD的面积.
(2)根据(1)中的函数解析式,利用配方法求出对称轴及顶点坐标.
(3)根据(1)中的函数解析式,求得B的坐标,然后根据S四边形ABCD=S△OAB+S△OBC+S△OCD即可求得四边形ABCD的面积.
解答:解:(1)根据题意,得
,
解得
,
∴所求二次函数的解析式为y=x2-4x-5;
(2)y=x2-4x-5;=(x-2)2-9,
∴顶点C坐标为(2,-9),
对称轴为直线x=2.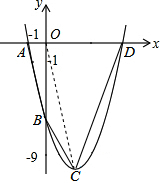
(3)∵二次函数的解析式为y=x2-4x-5,
∴B(0,-5),
连接OC,
S四边形ABCD=S△OAB+S△OBC+S△OCD=
×1×5+
×5×2+
×5×9=30.
|
解得
|
∴所求二次函数的解析式为y=x2-4x-5;
(2)y=x2-4x-5;=(x-2)2-9,
∴顶点C坐标为(2,-9),
对称轴为直线x=2.

(3)∵二次函数的解析式为y=x2-4x-5,
∴B(0,-5),
连接OC,
S四边形ABCD=S△OAB+S△OBC+S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法,四边形面积的求法等知识,难度中.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证: