题目内容
 如图,在直角坐标系中,矩形ABC0的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.求E点的坐标.
如图,在直角坐标系中,矩形ABC0的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.求E点的坐标.考点:翻折变换(折叠问题),坐标与图形性质
专题:
分析:如图,证明EA=EC(设为λ);根据勾股定理列出λ2=12+(3-λ)2,求得λ=
即可解决问题.
| 5 |
| 3 |
解答: 解:由题意知:∠BAC=∠DAC,AB∥OC,
解:由题意知:∠BAC=∠DAC,AB∥OC,
∴∠ECA=∠BAC,
∴∠ECA=∠DAC,
∴EA=EC(设为λ);由题意得:
OA=1,OC=AB=3;
由勾股定理得:λ2=12+(3-λ)2,
解得:λ=
,
∴OE=3-
=
,
∴E点的坐标为(0,
).
 解:由题意知:∠BAC=∠DAC,AB∥OC,
解:由题意知:∠BAC=∠DAC,AB∥OC,∴∠ECA=∠BAC,
∴∠ECA=∠DAC,
∴EA=EC(设为λ);由题意得:
OA=1,OC=AB=3;
由勾股定理得:λ2=12+(3-λ)2,
解得:λ=
| 5 |
| 3 |
∴OE=3-
| 5 |
| 3 |
| 4 |
| 3 |
∴E点的坐标为(0,
| 4 |
| 3 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
地球与太阳的平均距离大约为150000000km,这个数据用科学记数法表示正确的是( )
| A、1.5×107 |
| B、1.5×108 |
| C、15×108 |
| D、15×107 |
不等式组
的非负整数解有( )
|
| A、3个 | B、4个 | C、5个 | D、6个 |
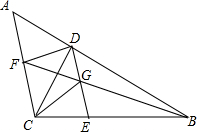 已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD.
已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD. 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证: