题目内容
4.已知关于x的方程kx2-3x+2=0有实数根,则k的取值范围是( )| A. | k$≤\frac{9}{8}$ | B. | k$>\frac{9}{8}$ | C. | k$≤\frac{9}{8}$且k≠0 | D. | k$<\frac{9}{8}$且k≠0 |
分析 分k=0即k≠0两种情况考虑,当k=0时,可求出x的值,由此得出k=0符合题意;当k≠0时,根据根的判别式△≥0可得出关于k的一元一次不等式,解之可得出k的取值范围,综上即可得出结论.
解答 解:当k=0时,原方程为-3x+2=0,
解得:x=$\frac{2}{3}$,
∴k=0符合题意;
当k≠0时,∵方程kx2-3x+2=0有实数根,
∴△=(-3)2-4×2k≥0,
解得:k≤$\frac{9}{8}$且k≠0.
综上所述:k的取值范围为k≤$\frac{9}{8}$.
故选A.
点评 本题考查了根的判别式以及解一元一次方程,分k=0即k≠0两种情况考虑是解题的关键.

练习册系列答案
相关题目
19.下列方程的变形中,正确的是( )
| A. | 若x-4=9,则x=8-4 | B. | 若2(2x+3)=2,则4x+6=2 | ||
| C. | 若-$\frac{1}{2}$x=4,则x=-2 | D. | 若$\frac{1}{3}$-$\frac{x-1}{2}$=1,则去分母得2-3(x-1)=1 |
8. 如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
 如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )| A. | 15个 | B. | 14个 | C. | 13个 | D. | 12个 |
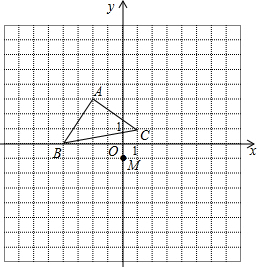 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,3),B(-4,0),C(1,1).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,3),B(-4,0),C(1,1).