题目内容
14.已知点A(2,2),B(-4,3),在x轴上求一点P,使PA+PB的和最小.分析 找出点A关于x轴的对称点A′,连接A′B与x轴交于点P,则P点即为所求,再根据点P在x轴上的位置得出P点坐标即可.
解答 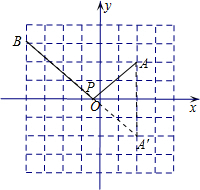 解:作点A关于x轴的对称点A′,连接A′B与x轴交于点P,则P点即为所求,
解:作点A关于x轴的对称点A′,连接A′B与x轴交于点P,则P点即为所求,
∵A(2,2),
∴A′(2,-2),
设直线A′B的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{2k+b=-2}\\{-4k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{5}{6}}\\{b=-\frac{1}{3}}\end{array}\right.$,
∴直线A′B的解析式为y=-$\frac{5}{6}$x-$\frac{1}{3}$,
令y=0,则-$\frac{5}{6}$x-$\frac{1}{3}$=0,
解得,x=-$\frac{2}{5}$,
∴P(-$\frac{2}{5}$,0).
点评 本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
5. 正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )
正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )
 正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )
正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )| A. | $5•{(\frac{3}{2})^{2013}}$ | B. | $5•{(\frac{3}{2})^{4026}}$ | C. | $5•{(\frac{3}{2})^{4028}}$ | D. | $5•{(\frac{3}{2})^{4030}}$ |
 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求:
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求: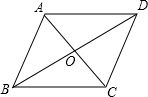 如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm.
如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm. 三角形ABC是直角三角形,AB是圆的直径,并且AB=20厘米.阴影①比阴影②的面积大18平方厘米,求BC的长度.
三角形ABC是直角三角形,AB是圆的直径,并且AB=20厘米.阴影①比阴影②的面积大18平方厘米,求BC的长度.