题目内容
13.高斯记号[x]表示不超过x的最大整数,即若有整数n满足n≤x<n+1,则[x]=n.当-1≤x<1时,请画出点P(x,x+[x])的纵坐标随横坐标变化的图象,并说明理由.分析 根据高斯记号[x]表示不超过x的最大整数,确定出点P(x,x+[x])的纵坐标随横坐标变化的分段函数解析式,画出图象即可.
解答  解:∵[x]表示不超过x的最大整数,
解:∵[x]表示不超过x的最大整数,
∴当-1≤x<0时,[x]=-1,P(x,x-1)
当0≤x<1时,[x]=0,P(x,x)
当x=1时,[x]=1,P(1,2)
图象变化如右图:
点评 本题考查了分段函数的图象及其性质,通过自变量的取值确定函数的解析式是本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
4.在△ABC中,AC=6,BC=8,AB=10,则点C到AB边的距离是( )
| A. | $\frac{24}{5}$ | B. | $\frac{5}{24}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
8.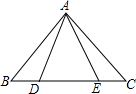 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )| A. | △ABD和△ACE成轴对称 | B. | △ABD和△ACE成中心对称 | ||
| C. | △ABD经过旋转可以和△ACE重合 | D. | △ABD经过平移可以和△ACE重合 |
5.礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A. | m+n | B. | mn+1 | C. | m+(n-1) | D. | n+(n+1) |
2.1微米=0.000001米,1微米用科学记数法可表示为( )米.
| A. | 1×106 | B. | 1×105 | C. | 1×10-5 | D. | 1×10-6 |
3.已知等式3a=5b-1,则下列等式中不一定成立的是( )
| A. | 3a-3=5b-4 | B. | 3a+b=6b-1 | C. | 3ac=5bc-1 | D. | b=$\frac{3a+1}{5}$ |
 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于E,若S△ABC=10,DE=3cm,AB=4cm,则AC的长为$\frac{8}{3}$cm.
如图,AD是△ABC中∠BAC的平分线,DE⊥AB于E,若S△ABC=10,DE=3cm,AB=4cm,则AC的长为$\frac{8}{3}$cm. 如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒.
如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒.