题目内容
12.计算:(1)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
(2)($\sqrt{6}$-$\sqrt{\frac{3}{2}}$)-($\sqrt{24}$-2$\sqrt{\frac{2}{3}}$)
(3)$\frac{2}{3}$$\sqrt{3\frac{3}{4}}$×(-9$\sqrt{45}$)
(4)5$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)÷$\sqrt{3}$.
分析 (1)首先化简二次根式进而合并求出即可;
(2)首先化简二次根式进而合并求出即可;
(3)利用二次根式的乘法运算法则化简求出即可;
(4)利用二次根式的除法运算法则化简求出即可.
解答 解:(1)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
$\sqrt{3}$-18$\sqrt{3}$+4
(2)($\sqrt{6}$-$\sqrt{\frac{3}{2}}$)-($\sqrt{24}$-2$\sqrt{\frac{2}{3}}$)
=$\sqrt{6}$-$\frac{\sqrt{6}}{2}$-2$\sqrt{6}$+$\frac{2\sqrt{6}}{3}$
=-$\frac{5\sqrt{6}}{6}$;
(3)$\frac{2}{3}$$\sqrt{3\frac{3}{4}}$×(-9$\sqrt{45}$)
=$\frac{2}{3}$×(-9)×3×$\sqrt{\frac{15}{4}×5}$
=-18×$\frac{5\sqrt{3}}{2}$
=-45$\sqrt{3}$;
(4)5$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)÷$\sqrt{3}$
=(20$\sqrt{3}$-18$\sqrt{3}$+4$\sqrt{15}$)÷$\sqrt{3}$
=(2$\sqrt{3}$+4$\sqrt{15}$)÷$\sqrt{3}$
=2+4$\sqrt{5}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
2. 如图所示,某计算装置有一数据的入口A和一运算结果的出口B.
如图所示,某计算装置有一数据的入口A和一运算结果的出口B.
下表是小刚输入一些数后所得的结果:
(1)若输出的数是5,则小刚输入的数是多少?
(2)若小刚输入的数是225,则输出的结果是多少?
(3)若小刚输入的数是n(n≥10),你能用含n的式子表示输出的结果吗?试一试.
 如图所示,某计算装置有一数据的入口A和一运算结果的出口B.
如图所示,某计算装置有一数据的入口A和一运算结果的出口B.下表是小刚输入一些数后所得的结果:
| A | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| B | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
(2)若小刚输入的数是225,则输出的结果是多少?
(3)若小刚输入的数是n(n≥10),你能用含n的式子表示输出的结果吗?试一试.
20. 如图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC的度数是( )
 如图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
 如图所示,已知∠DAC=∠ACB,∠D=62°,求∠BCD的度数.
如图所示,已知∠DAC=∠ACB,∠D=62°,求∠BCD的度数.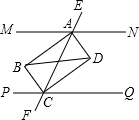 已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.