题目内容
3.所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使A=B2,则称A是完全平方式,例如:a4=(a2)2、4a2-4a+1=(2a-1)2.(1)下列各式中完全平方式的编号有①③⑥;
①a6;②x2+4x+4y2;③4a2+2ab+$\frac{1}{4}$b2;④a2-ab+b2;⑤x2-6x-9;⑥a2+a+0.25
(2)若4x2+5xy+my2和x2-nxy+$\frac{1}{4}$y2都是完全平方式,求(m-$\frac{1}{n}$)-1的值;
(3)多项式9x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请罗列出所有可能的情况,直接写答案)
分析 (1)利用完全平方公式的结构特征判断即可;
(2)利用完全平方公式的结构特征求出m与n的值,即可确定出原式的值;
(3)利用完全平方公式的结构特征判断即可.
解答 解:(1)①a6=(a2)3,是完全平方式;②x2+4x+4y2,不是完全平方式;③4a2+2ab+$\frac{1}{4}$b2=(2a+$\frac{1}{2}$b)2,是完全平方式;④a2-ab+b2,不是完全平方式;⑤x2-6x-9,不是完全平方式;⑥a2+a+0.25=(a+$\frac{1}{2}$)2,是完全平方式,
各式中完全平方式的编号有①③⑥;
(2)∵4x2+5xy+my2和x2-nxy+$\frac{1}{4}$y2都是完全平方式,
∴m=$\frac{25}{16}$,n=±1,
当n=1时,原式=$\frac{16}{9}$;当n=-1时,原式=$\frac{16}{41}$;
(3)单项式可以为-1,-9x2,6x,-6x,$\frac{81}{4}$x4.
点评 此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列各组数为勾股数的是( )
| A. | 5,12,13 | B. | 3,4,7 | C. | 4,7.5,8.5 | D. | 8,15,16 |
8.在平面直角坐标系中,△ABC顶点A(2,3).若以原点O为位似中心,画三角形ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为$\frac{2}{3}$,则A′的坐标为( )
| A. | $(3,\frac{9}{2})$ | B. | $(\frac{4}{3},6)$ | C. | $(3,\frac{9}{2})或(-3,-\frac{9}{2})$ | D. | $(\frac{4}{3},6)或(-\frac{4}{3},-6)$ |
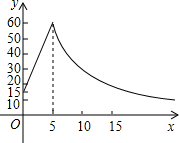 如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系.
如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系.