题目内容
2.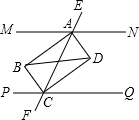 已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.(1)说说AB和CD、BC和AD的位置关系?
(2)你能判定四边形ABCD是矩形吗?为什么?
(3)AC和BD有怎样的大小关系?为什么?
分析 (1)首先推出∠BAC=∠DCA,继而推出AB∥CD;推出∠BCA=∠DAC,进而推出AD∥CB,因此四边形ABCD平行四边形,从而可以得到两组对边的关系;
(2)再证明∠ABC=90°,可得平行四边形ABCD是矩形;
(3)根据矩形的对角线相等即可得到答案.
解答 证明:(1)∵MN∥PQ,
∴∠MAC=∠ACQ、∠ACP=∠NAC
∵AB、CD分别平分∠MAC和∠ACQ,
∴∠BAC=$\frac{1}{2}$∠MAC、∠DCA=$\frac{1}{2}$∠ACQ,
又∵∠MAC=∠ACQ,
∴∠BAC=∠DCA,
∴AB∥CD,
∵AD、CB分别平分∠ACP和∠NAC,
∴∠BCA=$\frac{1}{2}$∠ACP、∠DAC=$\frac{1}{2}$∠NAC,
又∵∠ACP=∠NAC,
∴∠BCA=∠DAC,
∴AD∥CB,
又∵AB∥CD,
∴四边形ABCD平行四边形,
∴AB∥CD,AD∥BC;
(2)∵∠BAC=$\frac{1}{2}$∠MAC,∠ACB=$\frac{1}{2}$∠ACP,
又∵∠MAC+∠ACP=180°,
∴∠BAC+∠ACB=90°,
∴∠ABC=90°,
∴平行四边形ABCD是矩形.
(3)∵平行四边形ABCD是矩形,
∴AC=BD.
点评 此题主要考查了矩形的判定,关键是掌握有一个角是直角的平行四边形是矩形,属于基础题,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 画图并回答:
画图并回答: 如图,四边形ABCD是长方形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠ADE,点G是DF的中点,若BE=1,AG=3,则AB的长为2$\sqrt{2}$.
如图,四边形ABCD是长方形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠ADE,点G是DF的中点,若BE=1,AG=3,则AB的长为2$\sqrt{2}$.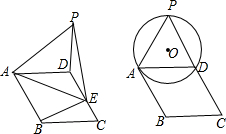 已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.
已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.