题目内容
12.某种子培育基地用A,B,C,D四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C型号种子的发芽率为95%,根据实验数据绘制了图-1和图-2两幅尚不完整的统计图.(1)请你将图-1中数据,图-2的统计图补充完整;
(2)培育基地进一步实验得知:发芽率最高的种子种地发芽之后,一粒发芽种子可收获0.1kg小麦,试问收获19kg小麦,大约需要发芽率最高的种子多少粒?

分析 (1)根据统计图可以得到D占的百分比和C型号种子的发芽数,从而可以将统计图补充完整;
(2)根据统计图可以计算出各种型号种子的发芽率,从而可以解答本题.
解答  解:(1)由扇形统计图可得,
解:(1)由扇形统计图可得,
D占的百分比为:1-35%-20%-20%=25%,
∵C型号种子的发芽率为95%,
∴C型号的种子发芽数为:2000×20%×95%=380,
故补全的图-1,图-2如右图所示,
(2)由题意可得,
A型号的发芽率是:$\frac{630}{2000×35%}$×100%=90%,
B型号的发芽率是:$\frac{370}{2000×20%}$×100%=92.5%,
C型号的发芽率是:95%,
D型号的发芽率是:$\frac{470}{2000×25%}$×100%=94%,
由上可得,发芽率最高的是C型号的种子,
19÷0.1÷95%=200(粒)
即大约需要发芽率最高的种子200粒.
点评 本题考查条形统计图、扇形统计图,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
相关题目
7. 如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )
如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )
 如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )
如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
3.某个函数自变量的取值范围是x≥-1,则这个函数的表达式为( )
| A. | y=x+1 | B. | y=x2+1 | C. | y=$\sqrt{x+1}$ | D. | y=$\frac{1}{x+1}$ |
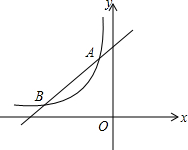 如图,直线y1=k1x+b与反比例函数${y_2}=\frac{k_2}{x}$(x<0)的图象相交于点A、点B,其中点A的坐标为(-2,4),点B的坐标为(-4,m).
如图,直线y1=k1x+b与反比例函数${y_2}=\frac{k_2}{x}$(x<0)的图象相交于点A、点B,其中点A的坐标为(-2,4),点B的坐标为(-4,m). 如图,矩形ABCD的对角线相交于点O,BD=6,AD=3$\sqrt{3}$,则∠AOD=120度.
如图,矩形ABCD的对角线相交于点O,BD=6,AD=3$\sqrt{3}$,则∠AOD=120度.