题目内容
20.计算:(1)(-1)0+($\frac{1}{3}$)-2+4×2-1;
(2)(3x-2)(x-1)
分析 (1)直接利用零指数幂的性质以及负整数指数幂的性质分别化简求出答案;
(2)直接利用多项式乘以多项式运算法则求出答案.
解答 解:(1)(-1)0+($\frac{1}{3}$)-2+4×2-1
=1+9+4×$\frac{1}{2}$
=12;
(2)(3x-2)(x-1)
=3x2-3x-2x+2
=3x2-5x+2.
点评 此题主要考查了零指数幂的性质以及负整数指数幂的性质和多项式乘以多项式运算等知识,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等边三角形 | B. | 菱形 | C. | 等腰直角三角形 | D. | 平行四边形 |
11.一元一次方程$\frac{2x+1}{3}$-$\frac{x-3}{6}$=1,去分母后得( )
| A. | 2(2x+1)-x-3=1 | B. | 2(2x+1)-x-3=6 | C. | 2(2x+1)-(x-3)=1 | D. | 2(2x+1)-(x-3)=6 |
12.抛物线y=ax2+bx+c的图象只经过第一、二象限,那么关于△=b2-4ac,下列结论成立的是( )
| A. | △<0 | B. | △≤0 | C. | △>0 | D. | △≥0 |
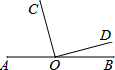 如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.
如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.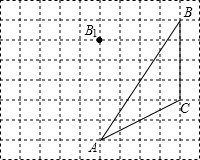 如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置.
如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置. 实数a,b在数轴上所对应的点的位置如图所示,用“<、>、=”等符号连接以下数字:2a<0,a+b>0,-|b-a|<0.
实数a,b在数轴上所对应的点的位置如图所示,用“<、>、=”等符号连接以下数字:2a<0,a+b>0,-|b-a|<0.