题目内容
2.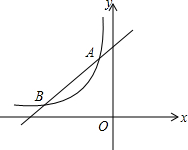 如图,直线y1=k1x+b与反比例函数${y_2}=\frac{k_2}{x}$(x<0)的图象相交于点A、点B,其中点A的坐标为(-2,4),点B的坐标为(-4,m).
如图,直线y1=k1x+b与反比例函数${y_2}=\frac{k_2}{x}$(x<0)的图象相交于点A、点B,其中点A的坐标为(-2,4),点B的坐标为(-4,m).(1)求出m,k1,k2,b的值;
(2)请直接写出 y1>y2时x的取值范围.
分析 (1)先根据点A的坐标,求得反比例函数解析式,再求得点B的坐标,最后根据待定系数法求得一次函数解析式即可;
(2)根据函数图象进行观察,写出一次函数图象在反比例函数图象上方时所有点的横坐标的集合即可.
解答 解:(1)∵点A(-2,4)在反比例函数${y_2}=\frac{k_2}{x}$图象上,
∴k2=-2×4=-8,
∴反比例函数解析式为${y_2}=\frac{-8}{x}$,
∵点B(-4,m)在反比例函数${y_2}=\frac{-8}{x}$图象上,
∴m=$\frac{-8}{-4}$=2,
∵点A(-2,4),点B(-4,2)在直线y1=k1x+b上,
∴$\left\{\begin{array}{l}{4=-2{k}_{1}+b}\\{2=-4{k}_{1}+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=1}\\{b=6}\end{array}\right.$;
(2)根据图象可得,当直线在双曲线的上方时,-4<x<-2,
∴当 y1>y2时,x的取值范围是:-4<x<-2.
点评 本题主要考查了反比例函数与一次函数的交点问题,需要掌握待定系数法求函数解析式的方法.解答此类试题的依据是:①函数图象的交点坐标满足函数解析式;②不等式的解集就是其所对应的函数图象上满足条件的所有点的横坐标的集合.

练习册系列答案
相关题目
13.在-1,π,$\sqrt{2}$,-$\sqrt{81}$中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列交通标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
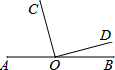 如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.
如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.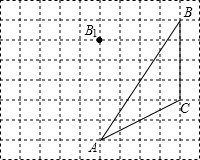 如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置.
如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置.