题目内容
17. 如图,矩形ABCD的对角线相交于点O,BD=6,AD=3$\sqrt{3}$,则∠AOD=120度.
如图,矩形ABCD的对角线相交于点O,BD=6,AD=3$\sqrt{3}$,则∠AOD=120度.
分析 由矩形的性质可推出∠ABC=90°,由特殊角的锐角三角函数值可求出∠ACB=30°,根据矩形性质求出OB=OC,求出∠OBC和∠OCB的度数,求出∠BOC,即可求出∠AOD.
解答 证明:∵四边形ABCD是矩形,
∴∠ABC=90°(矩形的四个角都是直角),BD=AC,AD=BC,
∵在Rt△ABC中,BD=6,AD=3$\sqrt{3}$,
∴cos∠ACB=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$,
∴∠ACB=30°,
∵四边形ABCD是矩形,
∴OB=OD=$\frac{1}{2}$BD,OC=OA=AC,AC=BD,
∴BO=CO,
∴∠OBC=∠OCB=30°,
∵∠OBC+∠OCB+∠BOC=180°,
∴∠BOC=120°,
∴∠AOD=∠BOC=120°,
故答案为:120.
点评 本题考查了等腰三角形性质,三角形的内角和定理,含30度角的直角三角形性质,矩形的性质的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
7.下列交通标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等边三角形 | B. | 菱形 | C. | 等腰直角三角形 | D. | 平行四边形 |
11.一元一次方程$\frac{2x+1}{3}$-$\frac{x-3}{6}$=1,去分母后得( )
| A. | 2(2x+1)-x-3=1 | B. | 2(2x+1)-x-3=6 | C. | 2(2x+1)-(x-3)=1 | D. | 2(2x+1)-(x-3)=6 |

 向某一容器中注水,注满为止,表示注水量与水深的函数关系的图象大致如图所示,则该容器可能是( )
向某一容器中注水,注满为止,表示注水量与水深的函数关系的图象大致如图所示,则该容器可能是( )



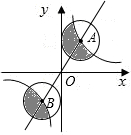 如图,正比例函数y=2x的图象和反比例函数$y=\frac{8}{x}$的图象相交于A、B两点,以A、B为圆心的两圆均与y轴相切,则图中阴影部分的面积之和等于( )
如图,正比例函数y=2x的图象和反比例函数$y=\frac{8}{x}$的图象相交于A、B两点,以A、B为圆心的两圆均与y轴相切,则图中阴影部分的面积之和等于( )