题目内容
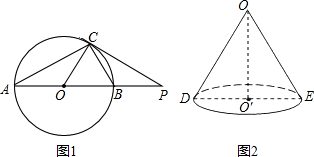
如图1,⊙O是Rt△ABC的外接圆,点P是AB延长线上一点,且OC⊥PC.
(1)求证:△PCA∽△PBC;
(2)若点B恰好是OP的中点,且⊙O的半径为R=5cm,试求出优弧BAC长;
(3)若以优弧BAC所围成的扇形面制作一个如图2的圆锥,试求出该圆锥的表面积.(π≈3,结果精确到个位)
(1)求证:△PCA∽△PBC;
(2)若点B恰好是OP的中点,且⊙O的半径为R=5cm,试求出优弧BAC长;
(3)若以优弧BAC所围成的扇形面制作一个如图2的圆锥,试求出该圆锥的表面积.(π≈3,结果精确到个位)

考点:圆的综合题
专题:
分析:(1)利用等腰三角形的性质以及两角互余的性质得出∠PCB=∠A,进而求出△PCA∽△PBC;
(2)利用直角三角形的性质以及等边三角形的判定得出∠AOC的度数,进而利用弧长公式求出即可;
(3)利用圆锥侧面展开图与底面圆的周长对应情况,进而得出其底面圆的半径,进而求出其表面积.
(2)利用直角三角形的性质以及等边三角形的判定得出∠AOC的度数,进而利用弧长公式求出即可;
(3)利用圆锥侧面展开图与底面圆的周长对应情况,进而得出其底面圆的半径,进而求出其表面积.
解答:(1)证明:由题意可得出:∠ACB=∠OCP=90°,
则∠ACO+∠OCB=90°,∠OCB+∠PCB=90°,
故∠ACO=∠PCB,
∵AO=CO,
∴∠OCA=∠OAC,
∴∠PCB=∠A,
又∵∠P=∠P,
∴△PCA∽△PBC;
(2)解:∵点B恰好是OP的中点,∠OCP=90°,
∴BC=OB=BP,
∴OC=OB=BC,
∴△COB是等边三角形,
∴∠COB=60°,
∴∠AOC=120°,
故优弧BAC长为:
=
π;
(3)解:∵优弧BAC长为:
π,
∴设圆锥底面圆的半径为:r,则其周长为:2πr=
π,
解得:r=
,
故该圆锥的表面积为:
+π×(
)2≈83(cm2).
则∠ACO+∠OCB=90°,∠OCB+∠PCB=90°,
故∠ACO=∠PCB,
∵AO=CO,
∴∠OCA=∠OAC,
∴∠PCB=∠A,
又∵∠P=∠P,
∴△PCA∽△PBC;
(2)解:∵点B恰好是OP的中点,∠OCP=90°,
∴BC=OB=BP,
∴OC=OB=BC,
∴△COB是等边三角形,
∴∠COB=60°,
∴∠AOC=120°,
故优弧BAC长为:
| 240π×5 |
| 180 |
| 20 |
| 3 |
(3)解:∵优弧BAC长为:
| 20 |
| 3 |
∴设圆锥底面圆的半径为:r,则其周长为:2πr=
| 20 |
| 3 |
解得:r=
| 10 |
| 3 |
故该圆锥的表面积为:
| 240π×52 |
| 360 |
| 10 |
| 3 |
点评:此题主要考查了相似三角形的判定与性质以及圆锥侧面展开图和扇形各部分对应情况,得出扇形圆心角度数是解题关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
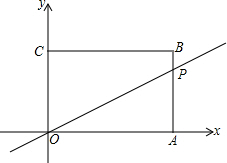 如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t
如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t 如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).
如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).
 如图,实数a、b在数轴上的位置,化简
如图,实数a、b在数轴上的位置,化简