题目内容
12.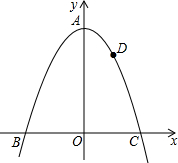 如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为3$\sqrt{2}$.
如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为3$\sqrt{2}$.
分析 由两点之间线段最短可知,当P点在线段BD上就可使PC+PD的值最小,解答即可.
解答 解:连接BD与y轴交于点P,
可得:PC+PD=BD,
把x=1,y=3代入y=-x2+k,解得:k=4,
把y=0代入y=-x2+4,解得:x=2或x=-2,
所以点B的坐标为(-2,0),
所以BD=$\sqrt{(-2-1)^{2}+{3}^{2}}=3\sqrt{2}$,
故答案为:3$\sqrt{2}$.
点评 本题考查了抛物线与x轴的交点,轴对称--最短路线问题,找到P点是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
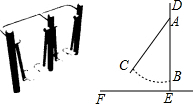 图中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°.求此时点C距离地面EF的高度.(结果精确到0.01m)【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】
图中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°.求此时点C距离地面EF的高度.(结果精确到0.01m)【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】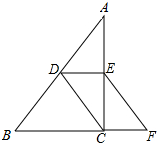 如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.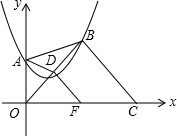 如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.
如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.