题目内容
16.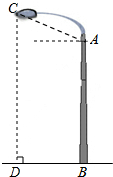 如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)
如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)【参考数据:sin20°=0.34,cos20°=0.94,tan20°=0.36】
分析 过点C作地面的垂线,垂足为D,过点A作AE⊥CD于E,在RT△ACE中,利用sin∠CAE=$\frac{CE}{AE}$,即可解决问题.
解答 解:如图,过点C作地面的垂线,垂足为D,过点A作AE⊥CD于E,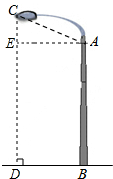 ∵∠EDB=∠ABD=∠AEB=90°,
∵∠EDB=∠ABD=∠AEB=90°,
∴四边形ABDE是矩形,
∴ED=AB=7.5,
∵∠CAE=∠CAB-90°=110°-90°=20°,
在RT△CAE中,∠AEC=90°,∠CAE=90°,∠CAE=20°,AC=1.7,
∵sin∠CAE=$\frac{CE}{AE}$,
∴CE=AE•sin∠CAE=1.7×0.34=0.578,
∴CD=CE+ED=0.578+7.5=8.078≈8.1米.
答:灯的顶端C距离地面的高度CD约为8.1米.
点评 本题考查解直角三角形的有关知识、矩形的判定和性质等知识,解题的关键是添加辅助线构造直角三角形以及矩形,学会转化的思想,把问题转化为直角三角形,特殊的四边形解决,属于中考常考题型.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
11. 如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
 如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
6.方程x2-ax+4=0的两根相等,则a=( )
| A. | 2 | B. | ±4 | C. | -4 | D. | 4 |
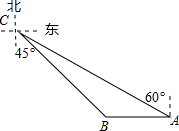 如图,码头A在码头B的正东方向,两个码头之间的距离为20海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.1海里)
如图,码头A在码头B的正东方向,两个码头之间的距离为20海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.1海里)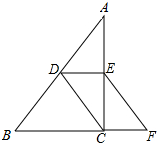 如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.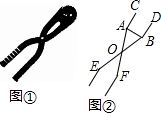 双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)
双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)