题目内容
11.在坐标系中,点O是坐标原点,抛物线y=-$\frac{1}{12}$x2+k的顶点M,直线y=-$\frac{1}{2}$x+b(b>0)分别与x轴,y轴交于点A和点B.点是AB的中点(1)若点P($\sqrt{3}$k,1)在抛物线上,求k的值;
(2)若抛物线y=-$\frac{1}{12}$x2+k经过点A和点B,求点C的坐标;
(3)把已知抛物线向右平移2个单位得到的新抛物线与直线y=-$\frac{1}{2}$x+b交于第一象限的P,Q两点,若新抛物线顶点恰好为点P,△OCQ的面积记为S,求S的取值范围.
分析 (1)把点P的坐标代入抛物线解析式,列出关于k的方程-$\frac{1}{12}$($\sqrt{3}$k)2+k=1,通过解方程求得k的值;
(2)利用直线解析式求得A(0,b),B(2b,0),所以根据中点坐标的求法不难得到C(b,$\frac{1}{2}$b),利用抛物线顶点坐标和二次函数图象上点的坐标特征得到抛物线y=-$\frac{1}{12}$x2+b经过点B,将点B的坐标代入二次函数解析式即可;
(3)平移后抛物线的顶点坐标为(2,k),将P(2,k)代入y=-$\frac{1}{2}$x+b上得:k=b-1,则新抛物线为y=-$\frac{1}{12}$(x-2)2+b-1,将y=-$\frac{1}{2}$x+b与y=-$\frac{1}{12}$(x-2)2+b-1联立可解得x的值,从而得到点Q的横坐标,然后依据S△OQC=S△BOQ-S△BOC得到S与b的函数关系式,最后利用S与b的函数关系式可确定出S的取值范围.
解答 解:(1)∵P($\sqrt{3}$k,1)在抛物线y=-$\frac{1}{12}$x2+k上,
∴-$\frac{1}{12}$($\sqrt{3}$k)2+k=1,
解得:k=2;
(2)由题意知A(0,b),B(2b,0),
∵C是AB的中点,
∴C(b,$\frac{1}{2}$b),
∵抛物线y=-$\frac{1}{12}$x2+k关于y轴对称,顶点坐标为(0,k),且经过点A,
∴抛物线y=-$\frac{1}{12}$x2+b经过点B,
∴0=-$\frac{1}{12}$(2b)2+b,
解得:b=3,
∴点C的坐标为(3,$\frac{3}{2}$);
(3)抛物线y=-$\frac{1}{12}$x2+k向右平移2个单位得到的新抛物线为y=-$\frac{1}{12}$(x-2)2+k,
∴抛物线的顶点坐标为(2,k).
∵顶点P(2,k)在直线y=-$\frac{1}{2}$x+b上,
∴k=-$\frac{1}{2}$×2+b,
∴k=b-1.
∴新抛物线为y=-$\frac{1}{12}$(x-2)2+b-1.
将y=-$\frac{1}{2}$x+b代入y=-$\frac{1}{12}$(x-2)2+b-1得:-$\frac{1}{2}$x+b=-$\frac{1}{12}$(x-2)2+b-1,
整理得:x2-10x+16=0,解得:x=2或x=8,
∴点Q的纵坐标为8.
∵S△OQC=S△BOQ-S△BOC,
∴S=$\frac{1}{2}$×BO×Qx-$\frac{1}{2}$×OB×Cx=$\frac{1}{2}$×b×8-$\frac{1}{2}$×b×b=-$\frac{1}{2}$b2+4b=-$\frac{1}{2}$(b-4)2+8.
∴S的取值范围是:0<S≤8.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了点的坐标与函数关系式的关系、二次函数的平移规律、二次函数的性质,列出S与b的函数关系式是解题的关键.

 阅读快车系列答案
阅读快车系列答案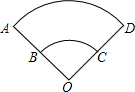 如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )
如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )| A. | 2倍 | B. | 4倍 | C. | $\frac{1}{2}$倍 | D. | $\frac{1}{4}$倍 |
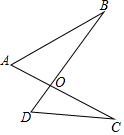 如图,不能判定△AOB和△DOC相似的条件是( )
如图,不能判定△AOB和△DOC相似的条件是( )| A. | AO•CO=BO•DO | B. | $\frac{AO}{DO}=\frac{AB}{CD}$ | C. | ∠A=∠D | D. | ∠B=∠C |
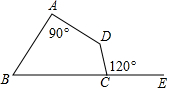 如图,延长四边形ABCD的BC边到E,∠DCE=120°,∠A=90°,∠D=2∠B.那么∠B的度数是( )
如图,延长四边形ABCD的BC边到E,∠DCE=120°,∠A=90°,∠D=2∠B.那么∠B的度数是( )| A. | 55° | B. | 60° | C. | 70° | D. | 80° |
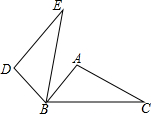 如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )| A. | 50° | B. | 70° | C. | 80° | D. | 90° |


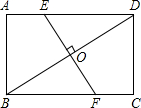 如图矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为$\frac{7}{8}$cm.
如图矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为$\frac{7}{8}$cm.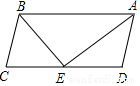 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的是⑤
如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的是⑤