题目内容
1.列一元一次方程解应用题为发展校园足球运动,某区四校决定联合购买100套队服和a(a≥10且为整数)个足球,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等.经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折
(1)求每套队服和每个足球的价格是多少?
(2)请用含a的式子分别表示出到甲商场所花的费用100a+14000元
乙商场购买装备所花的费用80a+15000元
(3)求出到甲、乙两家购买所需花的费用相同时a的值.
分析 (1)设每个足球的定价是x元,则每套队服是(x+50)元,根据两套队服与三个足球的费用相等列出方程,解方程即可;
(2)根据甲、乙两商场的优惠方案即可求解;
(3)由(2)的结论可得出关于a的一元一次方程,解之即可得出结论.
解答 解:(1)设每个足球的价格为x元,则每套队服的价格为(x+50)元,
根据题意得:2(x+50)=3x,
解得:x=100,
∴x+50=150.
答:每套队服的价格为150元,每个足球的价格为100元.
(2)到甲商场购买所花的费用为:150×100+100(a-$\frac{100}{10}$)=100a+14000(元),
到乙商场购买所花的费用为:150×100+0.8×100•a=80a+15000(元).
故答案为:100a+14000;80a+15000.
(3)根据题意得:100a+14000=80a+15000,
解得:a=50.
答:到甲、乙两家购买所需花的费用相同时a的值为50.
点评 本题考查了一元一次方程的应用,解题关键是:(1)根据两套队服与三个足球的费用相等列出方程;(2)根据两商城的优惠方案求出总费用;(3)根据两商城总花费相等列出方程.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
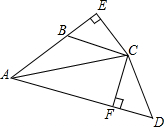 如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,E是AB延长线上一点,且CE⊥AE,CF⊥AD.
如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,E是AB延长线上一点,且CE⊥AE,CF⊥AD.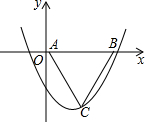 二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2的图象如图所示,若线段AB在x轴上,且AB=$\frac{4}{3}$$\sqrt{3}$,以AB为边作等边△ABC,使点C落在该函数第四象限的图象上,则点C的坐标是(0,-2)或(3,-2).
二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2的图象如图所示,若线段AB在x轴上,且AB=$\frac{4}{3}$$\sqrt{3}$,以AB为边作等边△ABC,使点C落在该函数第四象限的图象上,则点C的坐标是(0,-2)或(3,-2).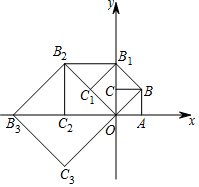 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B9的坐标为(0,32),点B2017的坐标为(0,21008)..
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B9的坐标为(0,32),点B2017的坐标为(0,21008)..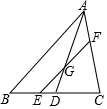 如图,点G是△ABC的重心,连结AG并延长交BC于点D,过点G作EF∥AB交BC于E,交AC于F.若AB=12,那么EF=8.
如图,点G是△ABC的重心,连结AG并延长交BC于点D,过点G作EF∥AB交BC于E,交AC于F.若AB=12,那么EF=8.