题目内容
17.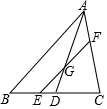 如图,点G是△ABC的重心,连结AG并延长交BC于点D,过点G作EF∥AB交BC于E,交AC于F.若AB=12,那么EF=8.
如图,点G是△ABC的重心,连结AG并延长交BC于点D,过点G作EF∥AB交BC于E,交AC于F.若AB=12,那么EF=8.
分析 由重心定理得到DG:DA=1:3,根据平行线分线段成比例定理证得$\frac{DE}{DB}$=$\frac{1}{3}$,再根据D是BC的中点化简得到$\frac{EF}{AB}$=$\frac{2}{3}$,把AB值代入即可.
解答 解:∵点G是△ABC的重心,
∴DG:AG=1:2,
∴DG:DA=1:3,
∵GE∥AB,
∴$\frac{EF}{AB}$=$\frac{CE}{CB}$,
∴$\frac{DG}{DA}$=$\frac{DE}{DB}$,即$\frac{DE}{DB}$=$\frac{1}{3}$,
∴$\frac{DE}{DB}$=$\frac{DE+DB}{DB}$=$\frac{4}{3}$,
∴$\frac{CE}{2DB}$=$\frac{2}{3}$,∴$\frac{CE}{CB}$=$\frac{2}{3}$,
∴$\frac{EF}{AB}$=$\frac{2}{3}$,
∵AB=12,
∴EF=8,
故答案为8.
点评 本题主要考查了三角形的重心以及平行线分线段成比例定理的综合应用,掌握重心到顶点的距离与重心到对边中点的距离之比为2:1是解题的关键.

练习册系列答案
相关题目
12.若$\sqrt{\frac{y+2}{2x-1}}$=$\frac{\sqrt{y+2}}{\sqrt{2x-1}}$,且x+y=5,则x的取值范围是( )
| A. | x$>\frac{1}{2}$ | B. | $\frac{1}{2}≤x<5$ | C. | $\frac{1}{2}≤x<7$ | D. | $\frac{1}{2}<x≤7$ |
2. 如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )
如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )
 如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )
如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )| A. | 20° | B. | 35° | C. | 130° | D. | 140° |
9.下列图形中,△ABC与△DEF不一定相似的是( )
| A. |  | B. |  | C. |  | D. |  |
7.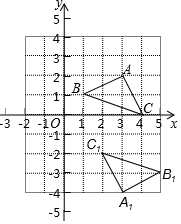 如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是( )
如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是( )
 如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是( )
如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是( )| A. | (3,1) | B. | (-3,-1) | C. | (3,-1) | D. | (-1,3) |
 (1)已知:如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点,求线段MN的长度.
(1)已知:如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点,求线段MN的长度.