Question

16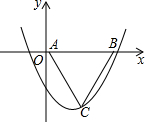．二次函数y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2的图象如图所示，若线段AB在x轴上，且AB=$\frac{4}{3}$$\sqrt{3}$，以AB为边作等边△ABC，使点C落在该函数第四象限的图象上，则点C的坐标是（0，-2）或（3，-2）．

Answer 1

分析 以AB为边的等边三角形，可求出该边上的高的长度，由于点C要落在二次函数的图象上，点C的纵坐标的绝对值即为AB边上的高的长度，从而可求出该点C的坐标

解答 解：设AB边上的高为h，
∵等边△ABC的边长为$\frac{4}{3}\sqrt{3}$，
∴AB边上的高h=2，
设点C的纵坐标为y，
∵点C在二次函数的图象上，
∴|y|=2，
∴y=±2，
∵点C落在该函数第四象限的图象上，
∴y=-2，
令y=-2代入y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2，
解得：x=0或3，
∴C的坐标为（0，-2）或（3，-2），
故答案为：（0，-2）或（3，-2）．

点评 本题考查了二次函数图象上的点特征以及等边三角形的性质，解题的关键是根据题意求出AB边上的高，从而得出C的纵坐标，本题属于中等题型．