题目内容
13.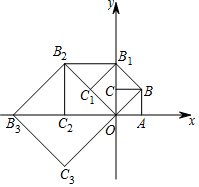 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B9的坐标为(0,32),点B2017的坐标为(0,21008)..
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B9的坐标为(0,32),点B2017的坐标为(0,21008)..
分析 首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标的之间的规律,然后根据规律计算出点B2017的坐标.
解答 解:∵正方形OABC边长为1,
∴OB=$\sqrt{2}$,
∵正方形OBB1C1是正方形OABC的对角线OB为边,
∴OB1=2,
∴B1点坐标为(0,2),
同理可知OB2=2$\sqrt{2}$,
∴B2点坐标为(-2,2),
同理可知OB3=4,B3点坐标为(-4,0),
B4点坐标为(-4,-4),B5点坐标为(0,-8),
B6(8,-8),B7(16,0)
B8(16,16),B9(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的$\sqrt{2}$倍,
∵2017÷8=252…1,
∴B2017的纵横坐标符号与点B1的相同,横坐标为0,纵坐标是正值,
∴B2017的坐标为(0,21008).
故答案为:(0,32),(21007,-21008).
点评 本题主要考查正方形的性质和坐标与图形的性质的知识点,解答本题的关键是由点坐标的规律发现每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的$\sqrt{2}$倍,此题难度较大

练习册系列答案
相关题目
12.若$\sqrt{\frac{y+2}{2x-1}}$=$\frac{\sqrt{y+2}}{\sqrt{2x-1}}$,且x+y=5,则x的取值范围是( )
| A. | x$>\frac{1}{2}$ | B. | $\frac{1}{2}≤x<5$ | C. | $\frac{1}{2}≤x<7$ | D. | $\frac{1}{2}<x≤7$ |
9.下列图形中,△ABC与△DEF不一定相似的是( )
| A. |  | B. |  | C. |  | D. |  |
10. 如图,已知AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)的个数有( )
如图,已知AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)的个数有( )
 如图,已知AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)的个数有( )
如图,已知AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)的个数有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
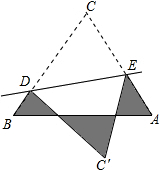 如图,在△ABC中,AC=BC=4cm,AB=6cm,D、E分别是BC、AC上的点,将△CDE沿直线DE折叠,点C落在点C′处,且C′在△ABC外部,则阴影部分图形的周长为14cm.
如图,在△ABC中,AC=BC=4cm,AB=6cm,D、E分别是BC、AC上的点,将△CDE沿直线DE折叠,点C落在点C′处,且C′在△ABC外部,则阴影部分图形的周长为14cm.