题目内容
6.已知点A(0,-4),B(8,0)和C(a,-a),若过点C的圆的圆心是线段AB的中点,则这个圆的半径的最小值是( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 利用点C的坐标可判断点C在直线y=-x上,在确定AB的中点D的坐标为(4,-2)过D点作DC垂直直线y=-x于点C,利用两点之间线段最短得到此时CD为过点C的圆的最小半径,再求出直线CD的解析式为y=x-6,
通过解方程组$\left\{\begin{array}{l}{y=-x}\\{y=x-6}\end{array}\right.$得C点坐标为(3,-3),然后利用两点的距离公式计算CD的长即可.
解答 解:∵C(a,-a),
∴点C在直线y=-x上,
设AB的中点D,则D(4,-2)
过D点作DC垂直直线y=-x于点C,此时CD为过点C的圆的最小半径,
∵CD⊥直线y=-x,
∴直线CD的解析式可设为y=x+b,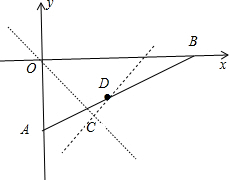
把D(4,-2)代入得4+b=-2,解得b=-6,
∴直线CD的解析式为y=x-6,
解方程组$\left\{\begin{array}{l}{y=-x}\\{y=x-6}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-3}\end{array}\right.$,
此时C点坐标为(3,-3),
∴CD=$\sqrt{(4-{3}^{2}+(-2+3)^{2}}$=$\sqrt{2}$,
即这个圆的半径的最小值为$\sqrt{2}$.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了坐标与图形性质.解决本题的关键是直线y=-x与圆相切时的切点坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.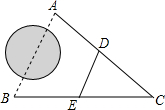 如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )
如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )
 如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )
如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )| A. | 60m | B. | 65m | C. | 70m | D. | 72m |
15. 如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )
如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )
 如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )
如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )| A. | 36° | B. | 44° | C. | 46° | D. | 54° |
 已知:如图,在?BEDF中,点A、C在对角线EF所在的直线上,且AE=CF.求证:四边形ABCD是平行四边形.
已知:如图,在?BEDF中,点A、C在对角线EF所在的直线上,且AE=CF.求证:四边形ABCD是平行四边形. 《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”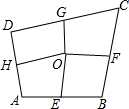 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.