题目内容
7.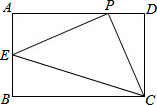 已知在矩形ABCD中,AB=2,BC=3,P是AD边上任意一点,(不含端点A、D),连接PC,过点P作PE⊥PC交AB于点E,在点P运动过程中,连接EC,是否存在∠ECP=∠DCP的情况?若存在,求出此时BE的长;若不存在,请说明理由.
已知在矩形ABCD中,AB=2,BC=3,P是AD边上任意一点,(不含端点A、D),连接PC,过点P作PE⊥PC交AB于点E,在点P运动过程中,连接EC,是否存在∠ECP=∠DCP的情况?若存在,求出此时BE的长;若不存在,请说明理由.
分析 作PM⊥CE于M,先由角平分线的性质得出PD=PM,再证出∠4=∠2,得出PA=PM,因此PA=PD=$\frac{1}{2}$AD,再由△APE∽△DCP,得出对应边成比例$\frac{AE}{PD}=\frac{PA}{CD}$,求出AE,即可得出BE.
解答 解:存在;作PM⊥CE于M,如图所示: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=CD=2,AD=BC=3,
∴∠1+∠2=90°,∠3+∠DCP=90°,
∵∠ECP=∠DCP,
∴PM=PD,
∵PE⊥PC,
∴∠CPE=90°,
∴∠4+∠ECP=90°,∠1+∠3=90°,
∴∠4=∠3,∠2=∠3,
∴∠4=∠2,
∴PA=PM,
∴PA=PD,
∴P为AD的中点,
∴PA=PD=$\frac{3}{2}$,
∵∠A=∠D,∠2=∠3,
∴△APE∽△DCP,
∴$\frac{AE}{PD}=\frac{PA}{CD}$,即$\frac{AE}{\frac{3}{2}}=\frac{\frac{3}{2}}{2}$,
∴AE=$\frac{9}{8}$,
∴BE=2-$\frac{9}{8}$=$\frac{7}{8}$.
点评 本题考查了矩形的性质、角的平分线的性质、相似三角形的判定与性质;熟练掌握矩形的性质,证明PA=PD是解决问题的关键.

练习册系列答案
相关题目
19.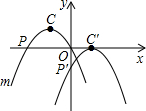 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )| A. | C(-$\frac{1}{2}$,$\frac{1}{2}$) | B. | C′(1,0) | C. | P(-1,0) | D. | P′(0,-$\frac{1}{2}$) |
16.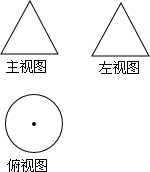 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | $\sqrt{3}$π |
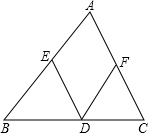 如图,在△ABC中,点D自点B向点C运动,作DE∥AC交AB于点E.作DF∥AB交AC于点F.
如图,在△ABC中,点D自点B向点C运动,作DE∥AC交AB于点E.作DF∥AB交AC于点F. 已知正方形的边长为a,内有一个内接圆,求阴影面积.
已知正方形的边长为a,内有一个内接圆,求阴影面积.