题目内容
10.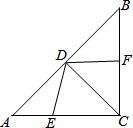 如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E、F分别是边AC、BC上的动点.AB=$\sqrt{32}$,设AE=x,BF=y.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E、F分别是边AC、BC上的动点.AB=$\sqrt{32}$,设AE=x,BF=y.(1)AC的长是4;
(2)若x+y=3,求四边形CEDF的面积;
(3)当DE⊥DF时,试探索x、y的数量关系.
分析 (1)根据锐角三角函数得到AC的长;
(2)如图,过点D作DG⊥AC于点G,DH⊥BC于点H,由∠ACB=90°,AC=BC,CD是∠ACB的角平分线得到∠A=∠B=∠ACD=∠BCD=45°,CD⊥AB,AD=CD=BD,在等腰直角三角形ACD中,DG⊥AC,∠A=45°求出DG=AG=$\frac{1}{2}$AC=2,DH=2,求出四边形CEDF的面积;
(3)当DE⊥DF时,∠EDF=90°,又因为CD⊥AB得到∠ADE+∠EDC=∠EDC+∠CDF=90°,证得△ADE≌△CDF,AE=CF,AE+BF=CF+BF=BC,即x+y=4.
解答 解:(1)在Rt△ABC中,∠ACB=90°,AC=BC,
∴AC=$\frac{\sqrt{2}}{2}$AB,
∵AB=$\sqrt{32}$,
∴AC=4;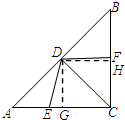
(2)如图,过点D作DG⊥AC于点G,DH⊥BC于点H
∵∠ACB=90°,AC=BC,CD是∠ACB的角平分线
∴∠A=∠B=∠ACD=∠BCD=45°,CD⊥AB
∴AD=CD=BD
∵在等腰直角三角形ACD中,DG⊥AC,∠A=45°
∴DG=AG=$\frac{1}{2}$AC=2
同理DH=2
∵S△CDE=$\frac{1}{2}$CE•DG=4-x,S△CDF=$\frac{1}{2}$CF•DH=4-y,
∴S四边形CEDF=S△CDE+S△CDF
=(4-x)+(4-y)=8-(x+y)=5;
(3)当DE⊥DF时,∠EDF=90°
∵CD⊥AB
∴∠ADE+∠EDC=∠EDC+∠CDF=90°
∴∠ADE=∠CDF,
又∵∠A=∠DCF=45°,
AD=CD
在△ADE与△CDF中,$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{AD=CD}\\{∠A=∠DCF}\end{array}\right.$,
∴△ADE≌△CDF
∴AE=CF
∴AE+BF=CF+BF=BC
即x+y=4.
点评 本题考查了等腰直角三角形的性质,三角形的面积公式,全等三角形的判定与性质,正确的作出辅助线是做题的关键.

 53随堂测系列答案
53随堂测系列答案 如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )
如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )| A. | 2cm | B. | 3cm | ||
| C. | 4cm | D. | 缺少条件,无法求出 |
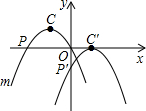 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )| A. | C(-$\frac{1}{2}$,$\frac{1}{2}$) | B. | C′(1,0) | C. | P(-1,0) | D. | P′(0,-$\frac{1}{2}$) |
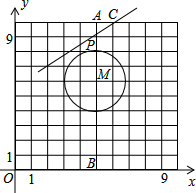 如图,点M的坐标为(5,6),⊙M的半径为2,点A,B,C都在网格的格点上,现有一点P在线段AB上运动.
如图,点M的坐标为(5,6),⊙M的半径为2,点A,B,C都在网格的格点上,现有一点P在线段AB上运动.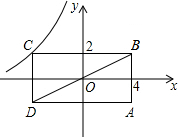 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.