题目内容
8.△ABC的一边长为5,另两边分别是方程x2-6x+m=0的两根,则m的取值范围是( )| A. | m>$\frac{11}{4}$ | B. | $\frac{11}{4}$<m≤9 | C. | $\frac{11}{4}$≤m≤9 | D. | m≤$\frac{11}{4}$ |
分析 设三角形另两边分别为a、b(a≥b),先利用判别式的意义得到m≤9,根据根与系数的关系得到a+b=6,ab=m,由于a<b+5,则利用完全平方公式变形得到(a-b)2<25,所以(a+b)2-4ab<25,即36-4m<25,解得m>$\frac{11}{4}$,于是可得到m的取值范围是$\frac{11}{4}$<m≤9.
解答 解:设三角形另两边分别为a、b(a≥b),
根据题意得△=(-6)2-4m≥0,解得m≤9,
a+b=6,ab=m,
∵a<b+5,即a-b<5,
∴(a-b)2<25,
∴(a+b)2-4ab<25,即36-4m<25,
∴m>$\frac{11}{4}$,
∴m的取值范围是$\frac{11}{4}$<m≤9.
故选B.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.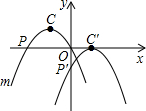 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )| A. | C(-$\frac{1}{2}$,$\frac{1}{2}$) | B. | C′(1,0) | C. | P(-1,0) | D. | P′(0,-$\frac{1}{2}$) |
16.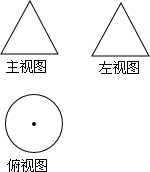 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | $\sqrt{3}$π |
3.关于m的不等式-m>1的解为( )
| A. | m>0 | B. | m<0 | C. | m<-1 | D. | m>-1 |
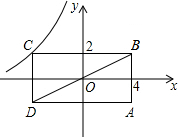 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.