题目内容
15．计算：$\sqrt{9}-\root{3}{-8}+4\sqrt{\frac{1}{4}}$．分析 先根据数的开方法则分别计算出各数，再根据实数混合运算的法则进行计算即可．
解答 解：原式=3+2+4×$\frac{1}{2}$
=5+2
=7．
点评 本题考查的是实数的运算，熟知数的开方法则是解答此题的关键．
练习册系列答案
相关题目
5．
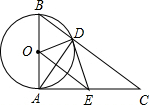如下图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．下面四个结论：
①ED是⊙O的切线；②BC=2OE；③△BOD为等边三角形；④△EOD∽△CAD
正确的是（ ）
如下图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．下面四个结论：①ED是⊙O的切线；②BC=2OE；③△BOD为等边三角形；④△EOD∽△CAD
正确的是（ ）
| A． | ①② | B． | ②④ | C． | ①②④ | D． | ①②③④ |
6．$\sqrt{（-4）^{2}}$的平方根是（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | ±4 |
3．在四个数$\sqrt{3}$，$\sqrt{2}$，1.7，2中，最大的是（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | 1.7 | D． | 2 |
10．
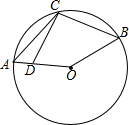如图，点C在$\widehat{AB}$上，点D在半径OA上，则下列结论正确的是（ ）
如图，点C在$\widehat{AB}$上，点D在半径OA上，则下列结论正确的是（ ）| A． | ∠DCB+$\frac{1}{2}$∠O=180° | B． | ∠ACB+$\frac{1}{2}$∠O=180° | C． | ∠ACB+∠O=180° | D． | ∠CAO+∠CBO=180° |
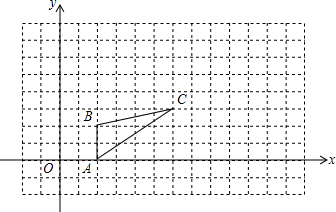如图，图中的小方格都是边长为1的正方形，△ABC的A、B、C三点坐标为A（2，0）、B（2，2）、C（6，3）．
5．
如图，两块直角三角板的直顶角O重合在一起，若∠BOC=$\frac{1}{5}$∠AOD，则∠BOC的度数为（ ）
如图，两块直角三角板的直顶角O重合在一起，若∠BOC=$\frac{1}{5}$∠AOD，则∠BOC的度数为（ ）| A． | 30° | B． | 45° | C． | 54° | D． | 60° |