题目内容
若2x=3,2y=5,求42x+y的值.
2025
【解析】试题分析：逆用幂的运算法则解答即可．
试题解析：【解析】
因为2x=3，2y=5，所以42x+y=42x×4y=24x×22y=（2x）4×（2y）2=34×52=2 025．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
如图,小敏做试题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,
然后粘贴在上面,她作图的依据是( )
A. SSS B. SAS C. ASA D. AAS
C
【解析】根据图形，可以确定两角及其夹边.故选C. 求满足下列条件的锐角θ的度数（精确到0.1°）：
（1）sinθ=0.1426；
（2）cosθ=0.7845．
（1）8.2°；（2）38.3°．
【解析】试题分析：（1）正确使用计算器计算即可．使用2nd键，然后按sin-1 0.1426即可求出θ的度数；（2）使用2nd键，然后按cos-1 0.7845即可求出θ的度数．
试题解析：
解：（1）∵sinθ=0.1426，∴∠θ≈8.2°；
（2）∵cosθ=0.7845，∴∠θ≈38.3°． 计算sin20°－cos20°的值是(精确到0.000 1)( )
A. －0.597 6 B. 0.597 6
C. －0.597 7 D. 0.597 7
C
【解析】按MODE，出现：DEG，按sin20?cos20=后，显示：?0.5977.
故选：C. 如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
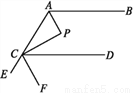
（1）∠CAP=90°-α； （2）证明见解析；（3）证明见解析；
【解析】试题分析：（1）由角平分线的定义可得∠PAC=α，在Rt△PAC中根据直角三角形的性质可求得∠ACP；
（2）结合（1）可求得∠ACD，可证明∠ACD+∠BAC=180°，可证明AB∥CD；
（3）由平行线的性质可得∠ECF=∠CAP，∠ECD=∠CAB，结合条件可证得∠ECF=∠FCD，可证得结论．
... 如图，在△ABC中，AB=AC，∠BAC = 36°，DE是线段AC的垂直平分线，若BE=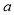
，AE=
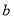，则用含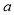、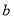的代数式表示△ABC的周长为 ．
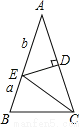
2a+3b
【解析】
试题分析：由题意可知：AC=AB=a+b，由于DE是线段AC的垂直平分线，∠BAC=36°，所以易证AE=CE=BC=b，从可知△ABC的周长△ABC的周长为：AB+AC+BC=2a+3b.
故答案为：2a+3b． 下列运算正确的是( )
A. (-2ab)·(-3ab)3=-54a4b4 B. 5x2·(3x3)2=15x12
C. (-0.1b)·(-10b2)3=-b7 D. (2×10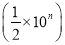n) 
=102n
D
【解析】解：A． 原式=54a4b4，故A错误；
B．原式=45x8，故B错误；
C． 原式=100b7，故C错误；
D．正确．
故选D． 不等式x－3＞1的解集是( )
A. x＞2 B. x＞4 C. x＞－2 D. x＞－4
B
【解析】试题分析：根据不等式的基本性质即可得到结果.
x－3＞1
x＞4
故选B. 如图，在△ABC中，AB=AD=DC，∠BAD=26°.求∠B和∠C的度数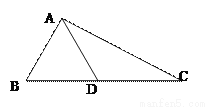
77° 38.5°
【解析】【解析】
∵ AB＝AD，
∴∠B＝∠ADB． ……………… 2分
∵在△ABD中，∠B+∠ADB+∠BAD＝180°，∠BAD＝26°，
∴∠B＝∠ADB＝77°． ……………… 4分
∵AD.＝DC，
∴∠DAC ＝∠C． ……………… 6分
∵∠ADB＝∠DAC+∠C， ……………… 7分
∴∠ADB＝2∠C，
...