题目内容
15.观察下列三组数据(三组数据个数一样),解答下列问题:①1,2,3,4,5,6,…,xn;
②3,4,5,6,7,8,…,yn;
③4,6,8,10,12,14,…,zn.
(1)根据你观察的结果,用含xn的代数式分别表示yn和zn;
(2)若设①组数据的平均数和方差分别为$\overline{{x}_{1}}$,s12,则②③组数据的平均数和方差各为多少?由此你能得出什么规律?
分析 (1)观察出①②、②③两组数的大小关系,用含xn的代数式分别表示yn和zn即可.
(2)首先根据平均数和方差的求法,分别求出②、③组数据的平均数和方差各为多少;然后根据求出的结果,总结出规律即可.
解答 解:(1)根据观察的结果,yn=xn+2;zn=xn+3.
(2)∵①组数据的平均数为$\overline{{x}_{1}}$,②组数据的每个数都加了2,
∴②组数据的平均数是$\overline{{x}_{1}}$+2,
∵①组数据的方差为s12,②组数据的每个数都加了2,
∴②组数据的波动不会变,方差不变,也是s12;
∵①组数据的平均数为$\overline{{x}_{1}}$,③组数据的每个数都加了3,
∴③组数据的平均数是$\overline{{x}_{1}}$+3,
∵①组数据的方差为s12,③组数据的每个数都加了3,
∴③组数据的波动不会变,方差不变,也是s12;
我得出的规律是:当一组数据都加上一个数(或减去一个数)时,平均数也加上或减去这个数,方差不变.
点评 此题主要考查了平均数和方差的含义和求法,要熟练掌握,解答此题的关键是要明确:当一组数据都加上一个数(或减去一个数)时,平均数也加上或减去这个数,方差不变.

练习册系列答案
相关题目
5.在△ABC中,∠C=90°,tanA=1,则∠B的度数是( )
| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
6.下列数值中,不是不等式$\frac{5}{2}$x≥2(x-3)+3的解的是( )
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
5. 如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
 如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )| A. | $\frac{15}{2}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{15}$ | D. | $\sqrt{55}$ |
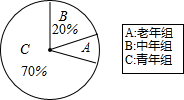 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人. 如图,在△ABC中,∠C=90°,BC、AC、AB边的长分别记为a、b、c,点E是BC边上一个动点(点E与点B、C不重合),连接AE.已知a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解.
如图,在△ABC中,∠C=90°,BC、AC、AB边的长分别记为a、b、c,点E是BC边上一个动点(点E与点B、C不重合),连接AE.已知a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解.