题目内容
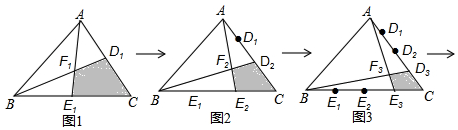
19.设△ABC的面积为1.如图1,分别将AC,BC边2等分,D1,E1是其分点,连接AE1,BD1交于点F1,得到四边形CD1F1E1,其面积S1=$\frac{1}{3}$.
如图2,分别将AC,BC边3等分,D1,D2,E1,E2是其分点,连接AE2,BD2交于点F2,得到四边形CD2F2E2,其面积S2=$\frac{1}{6}$;
如图3,分别将AC,BC边4等分,D1,D2,D3,E1,E2,E3是其分点,连接AE3,BD3交于点F3,得到四边形CD3F3E3,其面积S3=$\frac{1}{10}$;
…
按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CDnFnEn,其面积Sn=$\frac{2}{(n+1)(n+2)}$.
分析 先连接D1E1,D2E2,D3E3,依据D1E1∥AB,D1E1=$\frac{1}{2}$AB,可得△CD1E1∽△CBA,且$\frac{{D}_{1}{E}_{1}}{B{F}_{1}}$=$\frac{{D}_{1}{E}_{1}}{AB}$=$\frac{1}{2}$,根据相似三角形的面积之比等于相似比的平方,即可得到S△CD1E1=$\frac{1}{4}$S△ABC=$\frac{1}{4}$,依据E1是BC的中点,即可得出S△D1E1F1=$\frac{1}{3}$S△BD1E1=$\frac{1}{3}$×$\frac{1}{4}$=$\frac{1}{12}$,据此可得S1=$\frac{1}{3}$;运用相同的方法,依次可得S2=$\frac{1}{6}$,S2=$\frac{1}{6}$;根据所得规律,即可得出四边形CDnEnFn,其面积Sn=$\frac{1}{(n+1)^{2}}$+$\frac{1}{(n+1)^{2}}$×n×$\frac{1}{1+n+1}$,最后化简即可.
解答  解:如图所示,连接D1E1,D2E2,D3E3,
解:如图所示,连接D1E1,D2E2,D3E3,
∵图1中,D1,E1是△ABC两边的中点,
∴D1E1∥AB,D1E1=$\frac{1}{2}$AB,
∴△CD1E1∽△CBA,且$\frac{{D}_{1}{E}_{1}}{B{F}_{1}}$=$\frac{{D}_{1}{E}_{1}}{AB}$=$\frac{1}{2}$,
∴S△CD1E1=$\frac{1}{4}$S△ABC=$\frac{1}{4}$,
∵E1是BC的中点,
∴S△BD1E1=S△CD1E1=$\frac{1}{4}$,
∴S△D1E1F1=$\frac{1}{3}$S△BD1E1=$\frac{1}{3}$×$\frac{1}{4}$=$\frac{1}{12}$,
∴S1=S△CD1E1+S△D1E1F1=$\frac{1}{4}$+$\frac{1}{12}$=$\frac{1}{3}$,
同理可得:
图2中,S2=S△CD2E2+S△D2E2F2=$\frac{1}{9}$+$\frac{1}{18}$=$\frac{1}{6}$,
图3中,S3=S△CD3E3+S△D3E3F3=$\frac{1}{16}$+$\frac{3}{80}$=$\frac{1}{10}$,
以此类推,将AC,BC边(n+1)等分,得到四边形CDnEnFn,
其面积Sn=$\frac{1}{(n+1)^{2}}$+$\frac{1}{(n+1)^{2}}$×n×$\frac{1}{1+n+1}$=$\frac{2}{(n+1)(n+2)}$,
故答案为:$\frac{2}{(n+1)(n+2)}$.
点评 本题主要考查了图形的变化类问题以及三角形面积的计算,解决问题的关键作辅助线构造相似三角形,依据相似三角形的性质进行计算求解.解题时注意:相似三角形的面积之比等于相似比的平方.

| A. | 30×30 | B. | 40×40 | C. | 60×60 | D. | 80×80 |
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{19}$ | C. | $\frac{1}{\sqrt{5}}$ | D. | $\sqrt{8}$ |
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
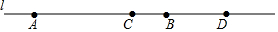 如图,直线l上有四点A、B、C、D,并且BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,如果AB、CD的中点分别为M、N,且MN=12cm,求线段AB的长.
如图,直线l上有四点A、B、C、D,并且BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,如果AB、CD的中点分别为M、N,且MN=12cm,求线段AB的长.