题目内容
9.某校九年级进行立定跳远训练,以下是刘明和张晓同学六次的训练成绩(单位:m)刘明:2.54,2.48,2.50,2.48,2.54,2.52
张晓:2.50,2.42,2.52,2.56,2.48,2.58
(1)填空:李明的平均成绩是2.51m.张晓的平均成绩是2.51m.
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?
(3)若预知参加年级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?请说明理由.
分析 (1)分别用两人的总成绩除以6,求出李明的平均成绩、张晓的平均成绩各是多少即可.
(2)首先根据方差的含义和求法,分别计算两人的六次成绩的方差;然后根据方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,判断出哪个人的成绩更稳定即可.
(3)判断出在6次成绩中,两人各有几次跳过2.55m,即可判断出应选哪个同学参加.
解答 解:(1)刘明的平均成绩为:$\frac{1}{6}$×(2.54+2.48+2.50+2.48+2.54+2.52)=2.51(m)
张晓的平均成绩为:$\frac{1}{6}$×(2.50+2.42+2.52+2.56+2.48+2.58)=2.51(m)
(2)S2刘明=$\frac{1}{6}$×[(2.54-2.51)2+(2.48-2.51)2+(2.50-2.51)2+(2.48-2.51)2+(2.54-2.51)2+(2.52-2.51)2]≈0.000 63
S2张晓=$\frac{1}{6}$×[(2.50-2.51)2+(2.42-2.51)2+(2.52-2.51)2+(2.56-2.51)2+(2.48-2.51)2+(2.58-2.51)2]≈0.002 77
∵S2刘明<S2张晓,
∴刘明的成绩更为稳定.
(3)若跳过2.55m就很可能获得冠军,则在6次成绩中,张晓2次都跳过了2.55 m,而刘明一次也没有,所以应选张晓参加.
故答案为:2.51m;2.51m.
点评 此题主要考查了方差的含义和求法,要熟练掌握,解答此题的关键是要明确:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.

练习册系列答案
相关题目
20.将分式$\frac{6m{n}^{3}}{4{m}^{3}n}$化成最简分式的结果正确的是( )
| A. | $\frac{6{n}^{2}}{4{m}^{2}}$ | B. | $\frac{6n}{4m}$ | C. | $\frac{3{n}^{2}}{2{m}^{2}}$ | D. | $\frac{3n}{2m}$ |
4.下列计算结果正确的是( )
| A. | (a3)2=a6 | B. | (-3a2)2=6a4 | C. | (-a2)3=a6 | D. | (-$\frac{1}{2}$ab2)3=$\frac{1}{8}$a3b6 |
18.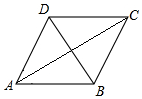 如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )
如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )
 如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )
如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )| A. | 50$\sqrt{3}$ | B. | 100$\sqrt{3}$ | C. | 200$\sqrt{3}$ | D. | 400$\sqrt{3}$ |
19.为了解某小区居民的日用电情况,居住在小区的一名同学随机抽查了15户家庭的日用电量,具体结果如下表所示:
则关于这15户家庭的日用电量,下列说法正确的是( )
| 日用电量/度 | 5 | 6 | 7 | 8 | 10 |
| 户数 | 2 | 5 | 4 | 3 | l |
| A. | 众数是10度 | B. | 平均数是7度 | C. | 中位数是6度 | D. | 中位数是7度 |