题目内容
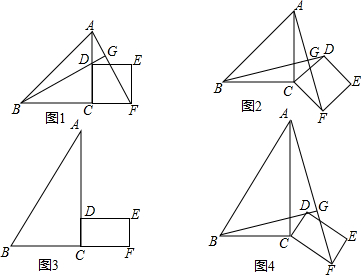
13.【探究】已知,Rt△ABC中,∠ACB=90°,AC=BC,四边形CDEF为正方形,BD、AF交于点G.
(1)若△ABC与正方形CDEF的位置如图1所示,试猜想BD、AF的位置关系,请直接写出结论:BD⊥AF;
(2)若将正方形CDEF绕点C顺时针旋转到图2所示的位置,(1)中的结论是否成立?并说明理由.
【拓展】
如图3,Rt△ABC中,∠ACB=90°,∠A=30°,AB=5,四边形CDEF为矩形,CD=1,CF=$\sqrt{3}$,若将矩形CDEF绕点C顺时针旋转到图4所示的位置,连接BD,AF交于点G,若∠DBC=15°,求AG的值.
分析 (1)由△BCD≌△ACF,推出∠DBC=∠CAF,由∠BDC+∠DBC=90°,∠BDC=∠ADG,推出∠DAG+∠ADG=90°,推出∠AGD=90°;
(2)结论仍然成立.由△BCD≌△ACF,推出∠DBC=∠CAF,由∠BOC+∠DBC=90°,∠BOC=∠AOG,推出∠OAG+∠AOG=90°,即可证明;
(3)由△BCD∽△ACF,推出∠DBC=∠CAF,由∠BOC+∠DBC=90°,∠BOC=∠AOG,推出∠OAG+∠AOG=90°,推出∠AGO=90°,BD⊥AF,由∠ABC=60°,∠GBC=15°,推出∠ABD=45°,推出△ABG是等腰直角三角形,即可解决问题;
解答 解:(1)结论:BD⊥AF.
理由:在△BCD和△ACF中,
$\left\{\begin{array}{l}{BC=BA}\\{∠BCD=∠ACF}\\{CD=CF}\end{array}\right.$,
∴△BCD≌△ACF,
∴∠DBC=∠CAF,
∵∠BDC+∠DBC=90°,∠BDC=∠ADG,
∴∠DAG+∠ADG=90°,
∴∠AGD=90°,
∴BD⊥AF.
故答案为BD⊥AF.
(2)结论仍然成立.
理由:如图2中,设AC与BD交于点O.
∵∠BCA=∠DCF=90°,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
$\left\{\begin{array}{l}{BC=BA}\\{∠BCD=∠ACF}\\{CD=CF}\end{array}\right.$,
∴△BCD≌△ACF,
∴∠DBC=∠CAF,
∵∠BOC+∠DBC=90°,∠BOC=∠AOG,
∴∠OAG+∠AOG=90°,
∴∠AGO=90°,
∴BD⊥AF.
(3)如图4中,设AC与BD交于点O.
∵∠BCA=∠DCF=90°,
∴∠BCD=∠ACF,
∵$\frac{BC}{AC}$=$\frac{DC}{CF}$=$\frac{\sqrt{3}}{3}$,
∴△BCD∽△ACF,
∴∴∠DBC=∠CAF,
∵∠BOC+∠DBC=90°,∠BOC=∠AOG,
∴∠OAG+∠AOG=90°,
∴∠AGO=90°,
∴BD⊥AF,
∵∠ABC=60°,∠GBC=15°,
∴∠ABD=45°,
∴△ABG是等腰直角三角形,
∴AG=$\frac{\sqrt{2}}{2}$AB=$\frac{5}{2}$$\sqrt{2}$.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、正方形的性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考常考题型.

| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
| 筹款金额(元) | 10 | 15 | 20 |
| 人数 | 10 | 17 | 13 |
| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
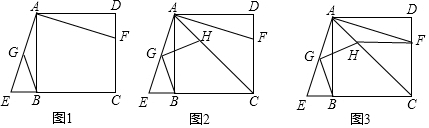
 如图多边形ABCDE的内角和是( )
如图多边形ABCDE的内角和是( )| A. | 360° | B. | 540° | C. | 720° | D. | 900° |
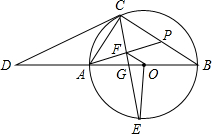 如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.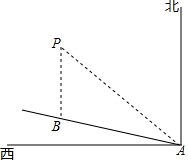 如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域,问这艘船能否按原方向继续向前航行?为什么?
如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域,问这艘船能否按原方向继续向前航行?为什么?