题目内容
若正数m、n满足m+4
-2
-4
+4n=3,则
= .
| mn |
| m |
| n |
| ||||
|
考点:二次根式的化简求值
专题:
分析:首先把方程整理为[(
)2+4
+(2
)2]-(2
+4
)-3=0,再根据相关的公式和提取公因式进行因式分解得:(
+2
)2-2(
+2
)-3=0,运用十字相乘法推出(
+2
-3)(
+2
+1)=0,即得
+2
=3,或者
+2
=-1(不符合题意,舍去),然后代入求值即可.
| m |
| mn |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
解答:解:∵m+4
-2
-4
+4n=3,
∴[(
)2+4
+(2
)2]-(2
+4
)-3=0,
∴(
+2
)2-2(
+2
)-3=0,
∴(
+2
-3)(
+2
+1)=0,
∴
+2
=3,或者
+2
=-1(不符合题意,舍去),
∵m、n为正数,
∴
+2
=-1(不符合题意,舍去),
∴原式=
=
.
故答案为
.
| mn |
| m |
| n |
∴[(
| m |
| mn |
| n |
| m |
| n |
∴(
| m |
| n |
| m |
| n |
∴(
| m |
| n |
| m |
| n |
∴
| m |
| n |
| m |
| n |
∵m、n为正数,
∴
| m |
| n |
∴原式=
| 3 |
| 3+3 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题主要考查用完全平方公式和式子相乘法分解因式,公因式的概念,二次根式的性质,关键在于题目中给出的方程确定
+2
的值,正确的代入原式进行计算求值.
| m |
| n |

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=
如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC= 如图,草坪上的自动喷水装置能旋转220°,若它的喷射半径是20m,则它能喷灌的草坪的面积为
如图,草坪上的自动喷水装置能旋转220°,若它的喷射半径是20m,则它能喷灌的草坪的面积为 如图,⊙O的弦AC、BD交于点Q,AP、CP是⊙O的切线,O、Q、P三点共线.求证:PA2=PB•PD.
如图,⊙O的弦AC、BD交于点Q,AP、CP是⊙O的切线,O、Q、P三点共线.求证:PA2=PB•PD.
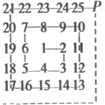 友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )
友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )