题目内容
 如图,⊙O的弦AC、BD交于点Q,AP、CP是⊙O的切线,O、Q、P三点共线.求证:PA2=PB•PD.
如图,⊙O的弦AC、BD交于点Q,AP、CP是⊙O的切线,O、Q、P三点共线.求证:PA2=PB•PD.考点:四点共圆
专题:证明题
分析:连接OA、OB、OD,设DP交⊙O于E.利用已知条件“AP、CP是⊙O的切线”可以证得A、O、C、P四点共圆;然后根据相交弦定理知OQ•PQ=AQ•CQ、DQ•BQ=AQ•CQ,由等量代换可以求得OQ•PQ=DQ•BQ,所以D、O、B、P四点共圆,所以由圆周角、弦、弧间的关系可以证得∠DPO=∠BPO,PB=PE;最后根据切割线定理得出结论PA2=PE•PD=PB•PD.
解答: 证明:连接OA、OB、OD、OC,设DP交⊙O于E.
证明:连接OA、OB、OD、OC,设DP交⊙O于E.
∵AP、CP是⊙O的切线,
∴∠OAP=∠PCO=90°
∴A、O、C、P四点共圆,
∴OQ•PQ=AQ•CQ(相交弦定理);
又∵DQ•BQ=AQ•CQ(相交弦定理),
∴OQ•PQ=DQ•BQ,
∴D、O、B、P四点共圆;
∵OD=OB,
∴∠ODB=∠OBD;
又∵ODPB四点共圆
∴∠ODB=∠OPB;∠OBD=∠OPD;
∴∠OPD=∠OPB,
∴PB=PE,
∴PA2=PE•PD=PB•PD(切割线定理),即PA2=PB•PD.
 证明:连接OA、OB、OD、OC,设DP交⊙O于E.
证明:连接OA、OB、OD、OC,设DP交⊙O于E.∵AP、CP是⊙O的切线,
∴∠OAP=∠PCO=90°
∴A、O、C、P四点共圆,
∴OQ•PQ=AQ•CQ(相交弦定理);
又∵DQ•BQ=AQ•CQ(相交弦定理),
∴OQ•PQ=DQ•BQ,
∴D、O、B、P四点共圆;
∵OD=OB,
∴∠ODB=∠OBD;
又∵ODPB四点共圆
∴∠ODB=∠OPB;∠OBD=∠OPD;
∴∠OPD=∠OPB,
∴PB=PE,
∴PA2=PE•PD=PB•PD(切割线定理),即PA2=PB•PD.
点评:本题考查了四点共圆的知识.把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆;或把被证共圆的四点两两连接并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积,即可肯定这四点也共圆.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
我校八年级安排部分同学外出社会实践活动,并将他们编成8个组,如果分配给每组的人数比预定人数多1名,那么外出学生总数超过100人;如果每组分配的人数比预定人数少1名,那么外出学生人数不到90人,则预定每组分配的人数为( )
| A、12人 | B、13人 |
| C、14人 | D、15人 |

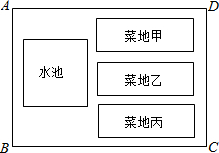 如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长.
如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长.