题目内容
 如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=
如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=考点:勾股定理,含30度角的直角三角形
专题:
分析:过A点作AD垂直BC于D点.因为BC=CD+BD,可先由∠B=60°,AD⊥BC,AB=10,求得BD=5,AD=5
,CD=7.进而在△ADC中根据勾股定理可求得AC的长.
| 3 |
解答: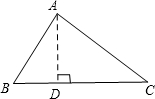 解:如图过A点作AD⊥BC于D点.
解:如图过A点作AD⊥BC于D点.
在Rt△ABD中,AB=10,∠B=60°.
∵cosB=
∴cos60°=
∴BD=10×cos60°=5,AD=
=5
.
∴CD=BC-BD=12-5=7,
在Rt△ADC中,AC=
=2
.
故答案为:2
.
 解:如图过A点作AD⊥BC于D点.
解:如图过A点作AD⊥BC于D点.在Rt△ABD中,AB=10,∠B=60°.
∵cosB=
| BD |
| 10 |
∴cos60°=
| BD |
| 10 |
∴BD=10×cos60°=5,AD=
| AB2-BD2 |
| 3 |
∴CD=BC-BD=12-5=7,
在Rt△ADC中,AC=
| AD2+CD2 |
| 31 |
故答案为:2
| 31 |
点评:此题考查了勾股定理,含30度角的直角三角形,涉及的知识点:三角函数和勾股定理.解题的关键是过A点作AD垂直BC于D点,构成直角三角形.

练习册系列答案
相关题目
小明掷一个质地均匀的正方体的骰子,骰子的六个面分别刻有1到6的点数,下列说法错误的是( )
| A、“正面出现点数大于6”是不可能事件 | ||
| B、“正面出现点数大于0”是必然事件 | ||
C、“正面出现点数是1”的概率是
| ||
D、“正面出现点数是偶数”的概率是
|
当n取遍大于1的所有自然数时,下列四个式子中所取的代数值总不出现完全平方数的是( )
| A、5n2-5n-5 |
| B、3n2-3n+3 |
| C、9n2-9n+9 |
| D、11n2-11n-11 |
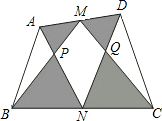 如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.
如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和. 数学大师化罗庚说过:“数形结合百般好,数形分离万事难”,图形是研究数学的重要工具,有一些复杂的运算若用图形表示出来,一看便知其结果.如计算:
数学大师化罗庚说过:“数形结合百般好,数形分离万事难”,图形是研究数学的重要工具,有一些复杂的运算若用图形表示出来,一看便知其结果.如计算: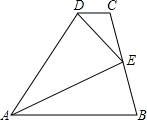 如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.