题目内容
已知△ABC中,∠BAC≠90°,AD⊥BC,BE⊥AC,且AD、BE交于点H,连接CH,则∠ACH+∠BAE= .
考点:四点共圆
专题:
分析:根据题意可知,点A、B、D、E共圆,点H是△ABC的垂心.过点A作⊙O的切线AF交BC的延长线BC于点F.根据切线的性质可知△ABF是直角三角形、由平行线的判定与性质可知∠HCA=∠CAF;最后由图形可知∠BAF=∠FAC+∠CAB=90°,即∠BAC+∠HCA=90°.
解答: 解:∵△ABC中,∠BAC≠90°,AD⊥BC,BE⊥AC,
解:∵△ABC中,∠BAC≠90°,AD⊥BC,BE⊥AC,
∴点A、B、D、E在以AB为直径的⊙O上;
过点A作⊙O的切线AF交BC的延长线BC于点F,则AF⊥AB.
∵点H是三角形ABC的垂心,
∴CH⊥AB,
∴CH∥AF,
∴∠HCA=∠CAF(两直线平行,内错角相等);
又∵∠BAF=∠FAC+∠CAB=90°,
∴∠BAC+∠HCA=90°.
故答案是:90°.
 解:∵△ABC中,∠BAC≠90°,AD⊥BC,BE⊥AC,
解:∵△ABC中,∠BAC≠90°,AD⊥BC,BE⊥AC,∴点A、B、D、E在以AB为直径的⊙O上;
过点A作⊙O的切线AF交BC的延长线BC于点F,则AF⊥AB.
∵点H是三角形ABC的垂心,
∴CH⊥AB,
∴CH∥AF,
∴∠HCA=∠CAF(两直线平行,内错角相等);
又∵∠BAF=∠FAC+∠CAB=90°,
∴∠BAC+∠HCA=90°.
故答案是:90°.
点评:本题考查了四点共圆的知识点.解答此题时,注意挖掘出隐含在题干中的已知条件点A、D、E、A共圆,点H是△ABC的垂心.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
小明掷一个质地均匀的正方体的骰子,骰子的六个面分别刻有1到6的点数,下列说法错误的是( )
| A、“正面出现点数大于6”是不可能事件 | ||
| B、“正面出现点数大于0”是必然事件 | ||
C、“正面出现点数是1”的概率是
| ||
D、“正面出现点数是偶数”的概率是
|
 数学大师化罗庚说过:“数形结合百般好,数形分离万事难”,图形是研究数学的重要工具,有一些复杂的运算若用图形表示出来,一看便知其结果.如计算:
数学大师化罗庚说过:“数形结合百般好,数形分离万事难”,图形是研究数学的重要工具,有一些复杂的运算若用图形表示出来,一看便知其结果.如计算:

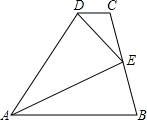 如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.