题目内容
方程7[x]-27{x}=1的解集是 .([x]表示不超过实数x的最大整数,{x}=x-[x],表示实数x的小数部分)
考点:取整计算
专题:
分析:首先将{x}=x-[x]代入方程,即可得到:x=
[x]-
,利用性质[x]≤x<[x]+1,即可确定[x]的取值,则可求得方程7[x]-27{x}=1的解集.
| 34 |
| 27 |
| 1 |
| 27 |
解答:解:∵7[x]-27{x}=1,{x}=x-[x],
∴7[x]-27(x-[x])=1,
∴x=
[x]-
,
∵[x]≤x<[x]+1,
∴[x]≤
[x]-
<[x]+1,
∴27[x]≤34[x]-1<27[x]+27,
∴
,
解得:
∴
≤[x]<4,
∴[x]=1,2,3,
∴方程7[x]-27{x}=1的解集为:
x1=
[x]-
=
×1-
=
,
x2=
[x]-
=
×2-
=
,
x3=
[x]-
=
×3-
=
,
故答案为:
,
,
.
∴7[x]-27(x-[x])=1,
∴x=
| 34 |
| 27 |
| 1 |
| 27 |
∵[x]≤x<[x]+1,
∴[x]≤
| 34 |
| 27 |
| 1 |
| 27 |
∴27[x]≤34[x]-1<27[x]+27,
∴
|
解得:
∴
| 1 |
| 7 |
∴[x]=1,2,3,
∴方程7[x]-27{x}=1的解集为:
x1=
| 34 |
| 27 |
| 1 |
| 27 |
| 34 |
| 27 |
| 1 |
| 27 |
| 33 |
| 27 |
x2=
| 34 |
| 27 |
| 1 |
| 27 |
| 34 |
| 27 |
| 1 |
| 27 |
| 67 |
| 27 |
x3=
| 34 |
| 27 |
| 1 |
| 27 |
| 34 |
| 27 |
| 1 |
| 27 |
| 101 |
| 27 |
故答案为:
| 33 |
| 27 |
| 67 |
| 27 |
| 101 |
| 27 |
点评:此题考查了取整函数的性质.注意性质[x]≤x<[x]+1与{x}=x-[x]的应用.

练习册系列答案
相关题目
多边形的边数增加2,这个多边形的内角和增加( )
| A、90° | B、180° |
| C、360° | D、540° |
小明掷一个质地均匀的正方体的骰子,骰子的六个面分别刻有1到6的点数,下列说法错误的是( )
| A、“正面出现点数大于6”是不可能事件 | ||
| B、“正面出现点数大于0”是必然事件 | ||
C、“正面出现点数是1”的概率是
| ||
D、“正面出现点数是偶数”的概率是
|
当n取遍大于1的所有自然数时,下列四个式子中所取的代数值总不出现完全平方数的是( )
| A、5n2-5n-5 |
| B、3n2-3n+3 |
| C、9n2-9n+9 |
| D、11n2-11n-11 |
 如图,四边形ABCD的对角线AC、BD相交于点O,
如图,四边形ABCD的对角线AC、BD相交于点O,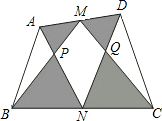 如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.
如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.