题目内容
13.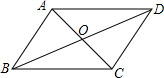 如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )
如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )| A. | 10 | B. | 11 | C. | 12 | D. | 22 |
分析 首先由平行四边形的性质可求出CD的长,由条件△OCD的周长为16,即可求出OD+OC的长,再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD=5,OA=OC,OB=OD,
∵△OCD的周长为16,
∴OD+OC=16-5=11,
∵BD=2DO,AC=2OC,
∴BD+AC=2(OD+OC)=22,
故选:D.
点评 本题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形的基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | x2+x3=x5 | B. | x4•x2=x6 | C. | (x2)3=x8 | D. | x6÷x2=x3 |
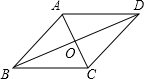 如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可)
如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可) 已知:如图,BC∥AD,∠A=∠B.
已知:如图,BC∥AD,∠A=∠B.
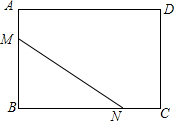 如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.
如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$. 将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=110°.
将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=110°.