Question

17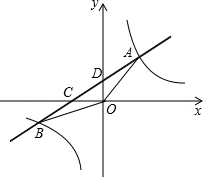．如图，在平面直角坐标系xOy中，一次函数y=$\frac{1}{2}$x+1的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于一、三象限内的A、B两点，直线AB与坐标轴交于C、D两点，△ADO的面积为2．
（1）求反比例函数的解析式；
（2）求△COB的面积．

Answer 1

分析 （1）过A作AE⊥y轴于E，过B作BF⊥x轴于F，由于直线y=$\frac{1}{2}$x+1与坐标轴交于C、D两点，于是得到C（-2，0），D（0，1），根据△ADO的面积为2，列方程求得AE=4，得到A（4，3），把A（4，3）代入y=$\frac{m}{x}$得到m=12，即可得到结论；
（2）解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=\frac{12}{x}}\end{array}\right.$得到$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=3}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=-6}\\{{y}_{2}=-2}\end{array}\right.$，求得B（-6，-2），根据三角形的面积公式即可得到结果．

解答 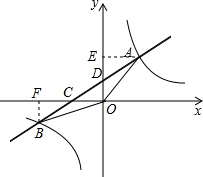解：（1）过A作AE⊥y轴于E，过B作BF⊥x轴于F，
∵直线y=$\frac{1}{2}$x+1与坐标轴交于C、D两点，
∴C（-2，0），D（0，1），
∵△ADO的面积为2，
∴$\frac{1}{2}$AE•OD=$\frac{1}{2}×AE×1$=2，
∴AE=4，
∵A在直线y=$\frac{1}{2}$x+1上，
∴A（4，3），
把A（4，3）代入y=$\frac{m}{x}$得：m=12，
∴反比例函数的解析式为：y=$\frac{12}{x}$；

（2）解$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=\frac{12}{x}}\end{array}\right.$得：$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=3}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=-6}\\{{y}_{2}=-2}\end{array}\right.$，
∴B（-6，-2），
∴△COB的面积=$\frac{1}{2}×$2×2=2．

点评 本题考查了一次函数和反比例函数的交点问题，用待定系数法求反比例函数的解析式的应用，求三角形的面积，主要考查学生的计算能力，题目比较好，难度适中．