题目内容
6. 如图,在?ABCD中,E是AD边的中点,EC交对角线BD于F,则EF:FC=1:2;△DFC的面积为8,则△DEF的面积为4.
如图,在?ABCD中,E是AD边的中点,EC交对角线BD于F,则EF:FC=1:2;△DFC的面积为8,则△DEF的面积为4.
分析 根据题意得出△DEF∽△BCF,进而得出$\frac{EF}{FC}=\frac{ED}{BC}=\frac{1}{2}$,然后根据△DFC与△DEF是同高的两个三角形可知S△DEF:S△DCF=EF:FC从而可求得△DEF的面积.
解答 解:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC.
∵E是AD边的中点,
∴$\frac{ED}{BC}=\frac{1}{2}$.
∵AD∥BC,
∴△DEF∽△BCF.
∴$\frac{EF}{FC}=\frac{ED}{BC}=\frac{1}{2}$.
∵△DFC与△DEF是同高的两个三角形,
∴S△DEF:S△DCF=EF:FC=1:2,即${S}_{△DEF}=\frac{1}{2}{S}_{DFC}$=$\frac{1}{2}×$8=4.
故答案为:1:2;4.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△DEF∽△BCF是解题关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
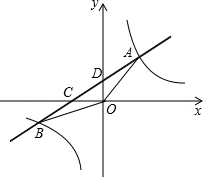 如图,在平面直角坐标系xOy中,一次函数y=$\frac{1}{2}$x+1的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,直线AB与坐标轴交于C、D两点,△ADO的面积为2.
如图,在平面直角坐标系xOy中,一次函数y=$\frac{1}{2}$x+1的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,直线AB与坐标轴交于C、D两点,△ADO的面积为2. 已知AB、BE、ED、CD依次相交于B、E、D,AB∥CD,试说明∠E=∠B+∠D.
已知AB、BE、ED、CD依次相交于B、E、D,AB∥CD,试说明∠E=∠B+∠D.