题目内容
9. 如图,BD,CE分别是△ABC的高,且BE=CD,求证:Rt△BEC≌Rt△CDB.
如图,BD,CE分别是△ABC的高,且BE=CD,求证:Rt△BEC≌Rt△CDB.
分析 根据高的定义求出∠BEC=∠CDB=90°,根据全等三角形的判定定理HL推出即可.
解答 证明:∵BD,CE分别是△ABC的高,
∴∠BEC=∠CDB=90°,
在Rt△BEC和Rt△CDB中,
$\left\{\begin{array}{l}{BC=BC}\\{BE=CD}\end{array}\right.$,
∴Rt△BEC≌Rt△CDB(HL).
点评 本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键.

练习册系列答案
相关题目
4.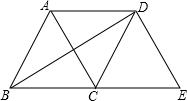 如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )
如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )
 如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )
如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.下列结论正确的是( )
| A. | -1乘以一个数得到这个数的相反数 | B. | |-$\frac{1}{7}$|×$\frac{1}{7}$=-$\frac{1}{49}$ | ||
| C. | -$\frac{1}{3}$×3=1 | D. | 几个有理数相乘,同号得正 |
19. 如图是一个立体图形的三种视图,根据视图所示数据计算该立体图形的体积为( )
如图是一个立体图形的三种视图,根据视图所示数据计算该立体图形的体积为( )
 如图是一个立体图形的三种视图,根据视图所示数据计算该立体图形的体积为( )
如图是一个立体图形的三种视图,根据视图所示数据计算该立体图形的体积为( )| A. | 250π | B. | 250 | C. | 125π | D. | 125 |
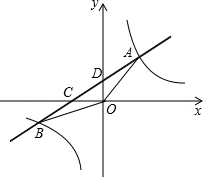 如图,在平面直角坐标系xOy中,一次函数y=$\frac{1}{2}$x+1的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,直线AB与坐标轴交于C、D两点,△ADO的面积为2.
如图,在平面直角坐标系xOy中,一次函数y=$\frac{1}{2}$x+1的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,直线AB与坐标轴交于C、D两点,△ADO的面积为2.