题目内容
2.已知一个等腰三角形的腰长2$\sqrt{5}$cm,底边长2$\sqrt{5}$cm,则这个等腰三角形的腰上的高的长为$\sqrt{15}$cm.分析 利用等边三角形的判定方法得出三角形是等边三角形,再利用勾股定理得出AD的长.
解答  解:如图所示,过点A作AD⊥BC于点D,
解:如图所示,过点A作AD⊥BC于点D,
∵一个等腰三角形的腰长2$\sqrt{5}$cm,底边长2$\sqrt{5}$cm,
∴三角形是等边三角形,
∴DC=$\sqrt{5}$cm,AC=2$\sqrt{5}$cm,
∴AD$\sqrt{A{C}^{2}-D{C}^{2}}$=$\sqrt{15}$(cm),
答:这个等腰三角形的腰上的高的长为$\sqrt{15}$cm.
故答案为:$\sqrt{15}$cm.
点评 此题主要考查了等边三角形的判定与性质以及勾股定理,正确应用等边三角形的性质是解题关键.

练习册系列答案
相关题目
13.用代入法解方程组$\left\{\begin{array}{l}{3x=2y+1}&\\{2x=3y}&\end{array}\right.$,以下各式中,代入正确的是( )
| A. | 3x=2×$\frac{2x}{3}$+1 | B. | 3x=2×$\frac{2y}{3}$+1 | C. | 3x=2×$\frac{3x}{2}$+1 | D. | 3x=2×6x+1 |
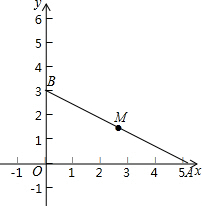 已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点.
已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点.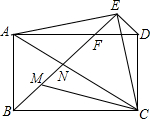 如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9.
如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9.