题目内容
6. 如图,△ABC中,∠A=80°,BD=BE,CD=CF.求∠EDF的度数.
如图,△ABC中,∠A=80°,BD=BE,CD=CF.求∠EDF的度数.
分析 如图,根据等腰三角形的性质可求得∠1=∠2∠3=∠4,再结合三角形内角和定理,可用∠B和∠C分别表示出∠2和∠4,结合平角的定义,可找到∠2+∠EDF+∠4=180°,可求得∠EDF的大小.
解答  解:∵∠A+∠B+∠C=180°,∠A=80°,
解:∵∠A+∠B+∠C=180°,∠A=80°,
∴∠B+∠C=100°,
∵BD=BE,CD=CF,
∴∠1=∠2∠3=∠4,
∵∠B+∠1+∠2=180°,∠C+∠3+∠4=180°,
∴∠2=$\frac{1}{2}$(180°-∠B),∠4=$\frac{1}{2}$(180°-∠C),
∵∠2+∠EDF+∠4=180°,
∴∠EDF=180°-∠2-∠4
=180°-$\frac{1}{2}$(180°-∠B)-$\frac{1}{2}$(180°-∠C)
=50°.
点评 本题主要考查等腰三角形的性质和三角形内角和定理,根据等边对等角和三角形内角和定理,找到∠B、∠C和∠EDF的关系是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14.某天同时同地,甲同学测得1m的测竿在地面上影长为0.8m,乙同学测得国旗旗杆在地面上的影长为9.6m,则国旗旗杆的长为( )
| A. | 10m | B. | 12m | C. | 13m | D. | 15m |
1.若等腰三角形的两边长分别是2和6,则这个三角形的周长是( )
| A. | 14 | B. | 10 | C. | 14或10 | D. | 以上都不对 |
 如图,点E,F在AC上,AB∥CD,AB=CD,AE=CF.求证:BF=DE.
如图,点E,F在AC上,AB∥CD,AB=CD,AE=CF.求证:BF=DE.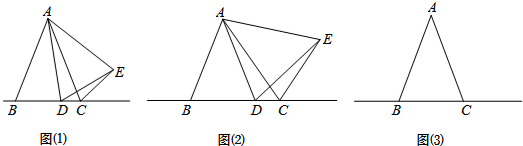
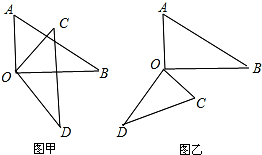 【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.
【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.