题目内容
11.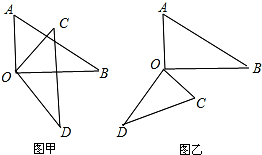 【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.
【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.(1)如果重叠在一起∠BOC=30°,猜想∠AOD=150°.
(2)如果将∠COD绕点O旋转,使重叠在一起的∠BOC=50°,则∠AOD=130°.
(3)如果将∠COD绕点O旋转,使重叠在一起的∠BOC=x°,则∠AOD=180°-x°.(用含x的式子表示)
(4)图甲中∠AOC与∠BOD满足的数量关系是,根据是∠AOC=∠BOD.
【拓展】在图甲所示的位置上,继续将∠COD绕点O旋转,得到如图乙所示的位置,请回答下面的问题.
(5)如果∠BOC=x°,则∠AOD=180°-x°.(用含x的式子表示)
(6)此时图乙中∠AOC与∠BOD始终满足的数量关系是相等,并说明理由.理由是:等量加等量,和相等.
【结论】
由上述的探究过程可知,三角板COD绕重合点O旋转.不论旋转到任何位置时,∠AOD与∠BOC始终满足的数量关系是∠AOD+∠BOC=180°.
分析 【探究】运用旋转变换的性质,结合几何图形,
(1)根据∠BOC=30°,直接猜测∠AOD=150°,即可解决问题.
(2)直接求出∠BOD,即可解决问题.
(3)表示出∠BOD,即可解决问题.
(4)运用公理:等量减等量差相等,即可解决问题.
【拓展】(5)首先表示出∠BOD,然后求出∠AOD,即可解决问题.
(6)运用公理:等量加等量和相等,即可判断结果.
【结论】运用周角=360°,求出∠AOD+∠BOC的度数,即可解决问题.
解答  解:【探究】(1)如图甲,如果重叠在一起∠BOC=30°,
解:【探究】(1)如图甲,如果重叠在一起∠BOC=30°,
猜想∠AOD=150°.
故答案为150°.
(2)∵∠BOC=50°,
∴∠BOD=40°,
∴∠AOD=130°.
故答案为130°.
(3)若∠BOC=x°,则∠BOD=90°-x°,
∴∠AOD=180°-x°.
故答案为180°-x°.
(4)如图甲,
∵∠AOC=90°-∠BOC,∠BOD=90°-∠BOC,
∴∠AOC=∠BOD.
故答案为∠AOC=∠BOD.
【拓展】(5)∵∠BOC=x°,
∴∠BOD=90°-x°,
∴∠AOD=180°-x°
故答案为180°-x°.
(6)如图乙,∵ ∠AOB=∠COD=90°,
∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
故答案为:相等.
理由是:等量加等量,和相等.
【结论】如图乙,∵∠AOB+∠COD=180°,
∴∠AOD+∠BOC=360°-180°=180°,
∴由上述的探究过程可知,三角板COD绕重合点O旋转.不论旋转到任何位置时,∠AOD与∠BOC始终满足的数量关系是:∠AOD+∠BOC=180°.
故答案为:∠AOD+∠BOC=180°.
点评 该题以旋转变换为方法,主要考查了角的计算及其规律的探究问题;抓住旋转过程中的不变元素,是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
3.已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=70°,∠BOC=50°,则∠AOC等于( )
| A. | 20° | B. | 60°或120° | C. | 120° | D. | 120°或20° |
20.下列计算正确的是( )
| A. | a+a=a2 | B. | a•a=a2 | C. | (a3)2=a5 | D. | a2•a3=a6 |
1.分式$\frac{1}{1-x}$有意义的条件是( )
| A. | x≠1 | B. | x>0 | C. | x≠-1 | D. | x<0 |
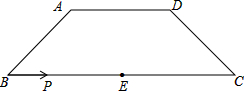 如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5cm,BC=12cm,CD=4cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了t秒
如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5cm,BC=12cm,CD=4cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了t秒 如图,△ABC中,∠A=80°,BD=BE,CD=CF.求∠EDF的度数.
如图,△ABC中,∠A=80°,BD=BE,CD=CF.求∠EDF的度数.