题目内容
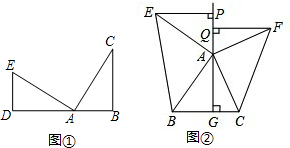
(1)如图①,点D、A、B正在一条直线上,∠D=∠B=90°,EA⊥AC,EA=AC.求证:AD=BC;
(2)如图②,在△ABC中,AG⊥AC于点G,以点A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰直角三角形BAE和等腰直角三角形CAF,过点E、F作射线GA的垂线,垂足分别为点P、Q,EP与FQ之间有怎样的数量关系?证明你的结论.
(2)如图②,在△ABC中,AG⊥AC于点G,以点A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰直角三角形BAE和等腰直角三角形CAF,过点E、F作射线GA的垂线,垂足分别为点P、Q,EP与FQ之间有怎样的数量关系?证明你的结论.

考点:全等三角形的判定与性质
专题:
分析:(1)求出∠EAC=∠D=∠B=90°,∠E=∠CAB,根据全等三角形的判定定理AAS推出即可;
(2)根据等腰直角三角形的性质得出∠FAC=∠EAB=90°,AC=AF,AE=AB,求出∠FQA=∠AGC=90°,∠QFA=∠GAC,根据AAS推出△AQF≌△CGA,推出FQ=AG,同理EP=AG,即可得出答案.
(2)根据等腰直角三角形的性质得出∠FAC=∠EAB=90°,AC=AF,AE=AB,求出∠FQA=∠AGC=90°,∠QFA=∠GAC,根据AAS推出△AQF≌△CGA,推出FQ=AG,同理EP=AG,即可得出答案.
解答:(1)证明:∵∠D=∠B=90°,EA⊥AC,
∴∠EAC=∠D=∠B=90°,
∴∠E+∠EAD=90°,∠EAD+∠CAB=90°,
∴∠E=∠CAB,
在△EDA和△ABC中,
,
∴△EDA≌△ABC(AAS),
∴AD=BC;
(2)EP=FQ,
证明:∵△BAE和△CAF是等腰直角三角形,
∴∠FAC=∠EAB=90°,AC=AF,AE=AB,
∵AG⊥BC,FQ⊥AG,
∴∠FQA=∠AGC=90°,
∴∠AFQ+∠QAF=90°,∠QAF+∠GAC=90°,
∴∠QFA=∠GAC,
在△AQF和△CGA中,
,
∴△AQF≌△CGA(AAS),
∴FQ=AG,
同理EP=AG,
∴FQ=EP.
∴∠EAC=∠D=∠B=90°,
∴∠E+∠EAD=90°,∠EAD+∠CAB=90°,
∴∠E=∠CAB,
在△EDA和△ABC中,
|
∴△EDA≌△ABC(AAS),
∴AD=BC;
(2)EP=FQ,
证明:∵△BAE和△CAF是等腰直角三角形,
∴∠FAC=∠EAB=90°,AC=AF,AE=AB,
∵AG⊥BC,FQ⊥AG,
∴∠FQA=∠AGC=90°,
∴∠AFQ+∠QAF=90°,∠QAF+∠GAC=90°,
∴∠QFA=∠GAC,
在△AQF和△CGA中,
|
∴△AQF≌△CGA(AAS),
∴FQ=AG,
同理EP=AG,
∴FQ=EP.
点评:本题考查了全等三角形的判定,三角形内角和定理,垂直定义的应用,解此题的关键是推出两三角形全等,题目比较典型,证明过程类似.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(x+y)2=x2+y2 |
| B、(-2x-y2)2=4x2-4xy+y2 |
| C、(m-n)(n-m)=-m2+2mn-n2 |
| D、(-2x+1)2=4x2+4x+1 |
 如图所示,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
如图所示,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点. 如图,AB是半圆的直径,BD是半圆的切线,C是半圆上任意一点,过C作BD的垂线,垂足为D,求证:AC是ED和AB的比例中项.
如图,AB是半圆的直径,BD是半圆的切线,C是半圆上任意一点,过C作BD的垂线,垂足为D,求证:AC是ED和AB的比例中项. 如图,AO⊥BO,CO⊥DO,∠AOD=160°,则∠BOC=
如图,AO⊥BO,CO⊥DO,∠AOD=160°,则∠BOC=