题目内容
如图，AB是半圆的直径，BD是半圆的切线，C是半圆上任意一点，过C作BD的垂线，垂足为D，求证：AC是ED和AB的比例中项．考点：切线的性质,相似三角形的判定与性质
专题：证明题
分析：根据切线的性质得出AB⊥BD，∠BAE=∠EBD，根据圆周角的性质得出∠AEB=90°，通过证得CD∥AB，根据平行弦的性质得出
=
，从而得出AC=BE，通过△ABE∽△BED，求得AB：BE=BE：ED，进而得出AB：AC=AC：ED．
 |
| AC |
|
| BE |
解答：解：∵AB是半圆的直径，BD是半圆的切线，
∴AB⊥BD，∠BAE=∠EBD，∠AEB=90°
∵CD⊥BD，
∴CD∥AB，
∴
=
，
∴AC=BE，
∵∠BAE=∠EBD，∠AEB=∠D=90°，
∴△ABE∽△BED，
∴AB：BE=BE：ED，
∴AB：AC=AC：ED，
即AC是ED和AB的比例中项．
∴AB⊥BD，∠BAE=∠EBD，∠AEB=90°
∵CD⊥BD，
∴CD∥AB，
∴
|
| AC |
|
| BE |
∴AC=BE，
∵∠BAE=∠EBD，∠AEB=∠D=90°，
∴△ABE∽△BED，
∴AB：BE=BE：ED，
∴AB：AC=AC：ED，
即AC是ED和AB的比例中项．
点评：本题考查了圆周角的性质，平行弦的性质，切线的性质等，熟练掌握和运用性质是解题的关键．
练习册系列答案
相关题目
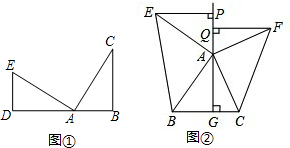
如图，正方形ABCD内有两点E、F满足AE=4，EF=FC=12，AE⊥EF，CF⊥EF，则正方形ABCD的边长为（ ）A、
| ||
B、10
| ||
| C、20 | ||
D、20
|
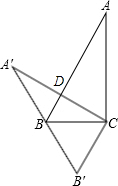在Rt△ABC中，∠ACB=90°，∠ABC=60°，将△ABC绕顶点C旋转到△A′B′C′的位置，使点B恰落在斜边A′B′上，设AC与AB相交于点D，则∠BDC=（ ）