题目内容
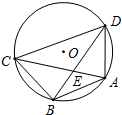如图，已知A、B、C、D是⊙O上的四个点，AB=BC，BD交AC于点E，连接CD、AD．（1）求证：DB平分∠ADC；
（2）若BE=3，ED=5，求AB的长．
考点：圆周角定理,相似三角形的判定与性质
专题：
分析：（1）等弦对等角可证DB平分∠ABC；
（2）易证△ABE∽△DBA，根据相似三角形的性质可求AB的长．
（2）易证△ABE∽△DBA，根据相似三角形的性质可求AB的长．
解答：（1）证明：∵AB=BC，
∴
=
，
∴∠BDC=∠ADB，
∴DB平分∠ADC；
（2）解：由（1）可知
=
，
∴∠BAC=∠ADB，
又∵∠ABE=∠ABD，
∴△ABE∽△DBA，
∴
=
，
∵BE=3，ED=5，
∴BD=8，
∴AB2=BE•BD=3×8=24，
∴AB=2
．
∴
 |
| AB |
|
| BC |
∴∠BDC=∠ADB，
∴DB平分∠ADC；
（2）解：由（1）可知
|
| AB |
|
| BC |
∴∠BAC=∠ADB，
又∵∠ABE=∠ABD，
∴△ABE∽△DBA，
∴
| AB |
| BE |
| BD |
| AB |
∵BE=3，ED=5，
∴BD=8，
∴AB2=BE•BD=3×8=24，
∴AB=2
| 6 |
点评：本题考查圆周角的应用，找出对应角证明三角形相似是本题的关键．
练习册系列答案
相关题目
若a+b=1，a-b=
，则a2-b2的值为（ ）
| 1 |
| 2 |
A、-
| ||
B、
| ||
| C、1 | ||
| D、2 |
如图所示，∠AOB=156°，OD是∠AOC的平分线，OE是∠BOC的平分线，那么∠DOE等于（ ）| A、78° | B、80° |
| C、88° | D、90° |
如图，已知点A（-4，4），点B为x轴的负半轴上的点，C为函数y=
如图，将三条线段CD，EF，GN分别绕点O旋转，不能与线段AB重合的线段是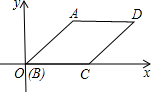
如图，?ABCD放入直角坐标系，BC在x轴上，且AB=4，BC=3，∠ABC=45°，则点D的坐标为
已知四边形OACB的四个顶点分别是O（0，0），B（3，3），C（6，0），A（3，-3）．在直角坐标系中画出这个四边形，并求这个四边形的面积．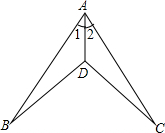
如图，∠1=∠2，由SAS判定△ABD≌△ACD，则需添加的条件