题目内容
14.计算:(3+1)(32+1)(34+1)…(31024+1)-$\frac{{3}^{2048}}{2}$.分析 将(3+1)(32+1)(34+1)…(31024+1)乘以$\frac{1}{2}$×(3-1)以配成平方差,再利用平方差公式计算即可.
解答 解:原式=$\frac{1}{2}$×(3-1)(3+1)(32+1)(34+1)…(31024+1)-$\frac{{3}^{2048}}{2}$
=$\frac{1}{2}$×(32048-1)-$\frac{{3}^{2048}}{2}$
=$\frac{{3}^{2048}}{2}$-$\frac{1}{2}$-$\frac{{3}^{2048}}{2}$
=-$\frac{1}{2}$.
点评 本题主要考查平方差公式,将原式乘以$\frac{1}{2}$×(3-1)以配成平方差是解题的技巧,熟悉平方差公式的构成特点是解题的关键.

练习册系列答案
相关题目
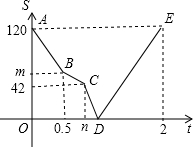 一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th后,与客车的距离为Skm,图中的折线(A→B→C→D→E)表示S与t之间的函数关系.
一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th后,与客车的距离为Skm,图中的折线(A→B→C→D→E)表示S与t之间的函数关系. 如图,矩形ABCD内接于⊙O,AB=2,AD=3,点P是⊙O上任一点,则sin∠APB的值为$\frac{2\sqrt{13}}{13}$.
如图,矩形ABCD内接于⊙O,AB=2,AD=3,点P是⊙O上任一点,则sin∠APB的值为$\frac{2\sqrt{13}}{13}$. 快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图.
快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图. 已知该抛物线y=x2+bx+c,经过点B(-4,0)和点A(1,0)与y轴交于点C.
已知该抛物线y=x2+bx+c,经过点B(-4,0)和点A(1,0)与y轴交于点C.