题目内容
2.过△ABC的三边中点D,E,F向内切圆引切线,设所引的切线分别与EF,FD,DE交于I,L,M.求证:I,L,M在一条直线上.分析 先用圆外切四边形的对角线以及对边切点连线四线共点判断出GC,PQ,BE共点,然后充分使用Menelaus定理,即可.
解答 解:如图,
设EL交AB于G,内切圆与AB,AC分别相切于P,Q.
连GC,PQ,BE,由圆外切四边形的对角线以及对边切点连线四线共点,设为点O.记BC=a,CA=b,AB=c.
由切线长定理不难算得AP=QA=$\frac{b+c-a}{2}$,
进而PB=$\frac{c+a-b}{2}$,QE=QA-EA=$\frac{c-a}{2}$.
∵P,O,Q共线,
∴$\frac{BO}{OE}×\frac{EQ}{QA}×\frac{AP}{PB}$=1 (对△BEA使用Menelaus定理),
∴$\frac{BO}{OE}=\frac{PB}{EQ}$=$\frac{c+a-b}{c-a}$,
∵G,O,C共线,
∴$\frac{BO}{OE}×\frac{EC}{CA}×\frac{AG}{GB}$=1 (对△BEA使用Menelaus定理),
∴$\frac{GB}{AG}=\frac{1}{2}×\frac{BO}{OE}$=$\frac{c+a-b}{2c-2a}$,
∴$\frac{GF}{AF}=\frac{AF-AG}{AF}=\frac{AB-2AG}{AB}=\frac{AG+BG-2AG}{AG+BG}$=$\frac{GB-AG}{GB+AG}$=$\frac{c+a-b}{2c-2a}$,
∵DE∥AB,DL∥AC (中位线定理),
∴$\frac{FL}{LD}=\frac{GL}{LE}=\frac{GF}{FA}$=$\frac{3a-b-c}{3c-a-b}$,
同理,在原题图形中可得$\frac{DM}{ME}=\frac{3b-c-a}{3a-b-c}$,$\frac{EI}{IF}=\frac{3c-a-b}{3b-a-c}$
∴$\frac{FL}{LD}×\frac{DM}{ME}×\frac{EI}{IF}$=1.
即:点I,L,M共线,(对△FDE使用Menelaus定理).
点评 此题是三角形五心题,主要考查了,圆外切四边形的对角线以及对边切点连线四线共点,Menelaus定理,解本题的关键是GC,PQ,BE共点.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案

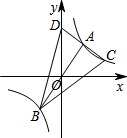 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.