题目内容
解方程组:
.
|
考点:高次方程
专题:
分析:先由第一个方程得出9a2+4b2=a2b2③,由第二个方程得出a2=b2+4④,再将④代入③,消去a,得到关于b的方程,解方程求出b的值,进而求a即可.
解答:解:
,
由①得9a2+4b2=a2b2③,
由②得a2=b2+4④,
将④代入③,得9(b2+4)+4b2=(b2+4)b2,
整理得b4-9b2-36=0,
(b2-12)(b2+3)=0,
∵b2+3>0,
∴b2-12=0,
∴b=±2
,
∴a2=b2+4=12+4=16,
∴a=±4.
经检验,
,
,
,
都是原方程组的解,
故原方程组的解是
,
,
,
.
|
由①得9a2+4b2=a2b2③,
由②得a2=b2+4④,
将④代入③,得9(b2+4)+4b2=(b2+4)b2,
整理得b4-9b2-36=0,
(b2-12)(b2+3)=0,
∵b2+3>0,
∴b2-12=0,
∴b=±2
| 3 |
∴a2=b2+4=12+4=16,
∴a=±4.
经检验,
|
|
|
|
故原方程组的解是
|
|
|
|
点评:本题考查了高次方程的解法,题中将第一个分式方程转化为整式方程以后,通过消去一个未知数a,得到一个一元四次方程b4-9b2-36=0,这是解题的关键.注意解分式方程要进行检验.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
在△ABC中,∠A=60°,且∠B:∠C=1:3,则这个三角形一定是( )
| A、等边三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
十年后,909班学生聚会,见面时相互间均握了一次手,好事者统计:一共握了780次.你认为这次聚会的同学有( )人.
| A、38 | B、39 | C、40 | D、41 |
 如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.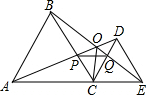 如图,C为AE上一点,在AE同侧分别作等边△ABC和等边△CDE,AD与BC交于点P,BE与CD交于Q,连接PQ.求证:∠AOB=60°.
如图,C为AE上一点,在AE同侧分别作等边△ABC和等边△CDE,AD与BC交于点P,BE与CD交于Q,连接PQ.求证:∠AOB=60°.