题目内容
十年后,909班学生聚会,见面时相互间均握了一次手,好事者统计:一共握了780次.你认为这次聚会的同学有( )人.
| A、38 | B、39 | C、40 | D、41 |
考点:一元二次方程的应用
专题:
分析:设这次聚会的同学有x人,每名同学要握手(x-1)次,共握手x(x-1)次,但是每两名同学只握手一次,需将重复计算的握手次数去掉,即共握手
x(x-1)次,然后根据一共握手780次就可以列出方程解决问题.
| 1 |
| 2 |
解答:解:设这次聚会的同学有x人,
依题意得,
x(x-1)=780,
∴x2-x-1560=0,
∴x1=40,x2=-39(负值舍去).
答:这次聚会的同学有40人.
故选:C.
依题意得,
| 1 |
| 2 |
∴x2-x-1560=0,
∴x1=40,x2=-39(负值舍去).
答:这次聚会的同学有40人.
故选:C.
点评:考查了一元二次方程的应用,此题和实际生活结合比较紧密,正确理解题意,找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.最后要判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
相关题目
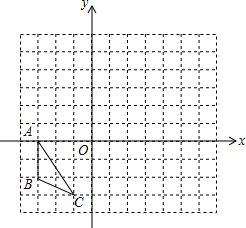 如图,在边长为1的正方网格内有一个三角形ABC.
如图,在边长为1的正方网格内有一个三角形ABC.