题目内容
在△ABC中，∠A=60°，且∠B：∠C=1：3，则这个三角形一定是（ ）
| A、等边三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
考点：三角形内角和定理
专题：
分析：首先设出∠B=x°，表示出∠C=3x°，利用三角形的内角和180°，列方程求得各个角的度数，进一步判断得出答案即可．
解答：解：∵在△ABC中，∠A=60°，且∠B：∠C=1：3，
∴设∠B=x°，∠C=3x°．
∵∠A+∠B+∠C=180°，
∴60+x+3x=180，
∴x=30，
∴∠B=30°，∠C=90°，
∴△ABC是直角三角形．
故选：B．
∴设∠B=x°，∠C=3x°．
∵∠A+∠B+∠C=180°，
∴60+x+3x=180，
∴x=30，
∴∠B=30°，∠C=90°，
∴△ABC是直角三角形．
故选：B．
点评：本题考查了三角形内角和定理．求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
菱形ABCD的对角线交于点O，同时菱形中的两条线段也交于点O，探索当∠EOF具有怎样的特征时，EM=NF，并说明理由．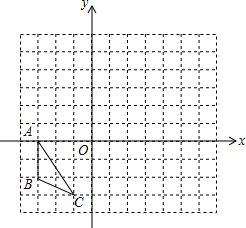
如图，在边长为1的正方网格内有一个三角形ABC．